Introduction to Statistics
Basic Terminology
In order to accomplish a statistical analysis, we first have to gather data from some source. In statistics, this source of data is called population. Don't be confused that it has to represent only people! A population in statistics can represent anything, for example: measurements of forest fires, stock market prices, sun activity and among others, people.
What if we want to name only a smaller part from a population? Then we call it a sample. A sample is normally a subset of the manageable size which is extracted from the population.
Descriptive vs. inferential
We can divide the study of statistics into two general branches: descriptive and inferential.
Inferential statistics is based on the probability theory as the result of its computation is still a probability. With inferential statistics we infer patterns and trends about a population. We construct those patterns based on an analysis of an individual sample from the population. Inferential statistics helps us to generalize better about a population.
How can we analyze every member of the population individually? Well, it's quite a tedious task ... What we can do to make our life easier is to choose a sample that represents the population the most and infer in the peculiarities of the population. Those peculiarities from the population we want to study are built on this representative sample.
As an example, imagine we want to analyze hours spent studying from all students in Germany. Trying to measure study hours of so many people is extremely challenging. By the time we are done with our analysis, some students may graduate or some new students with different habits may come in. In any case, we end up with a lot of calculations, if we work with the whole data set (with the population). Moreover, gathering so much information is rather difficult and time consuming. Even if we had the perfect data set, it wouldn't ease the task much.
What we can do is to take only one sample consisting of, let's say, 10.000 students chosen at random. Now we can focus on studying these particular people who will represent the whole "student population" of Germany which is approx. 2.7M . Now we can make inferences from our sample and afterwards generalize those inferences in respect to the whole set of students.
Descriptive statistics is what its name says: it describes the data which comes from a sample and filters out not meaningful information. From now on, we will talk about descriptive statistics more in detail.
Descriptive Statistics: diving into the terminology.
In descriptive statistics we have different metric groups to describe data. One metric group is called "measures of central tendency" and the other group "measures of variability".
Measures of Central Tendency
Let's start with the metrics of central tendency. The three measures of central tendency are: mean, median and mode. These measures are normally a single number and are applied to mainly describe the center of data.
Mean
The mean value is the average value of the data. This is the number which summarizes the entire data set most precisely.
The mean of a population is denoted by the Greek letter μ (pronounced as mju). We can compute the mean over the whole population or over a sample:



Note: The mean will always change if any data value in the data set changes.
The problem with the mean is that it is outlier-sensitive. Outliers are values that are unexpectedly different from the rest. They are an anomaly. Those values are normally either extremely small or extremely large. Such outliers cause skewed distributions and drag the mean towards the outlier, so the mean becomes not representative for the middle point of the data set.
For example, if we compare the yearly income of workers of the company B, we will get the following mean:

It seems to represent the average salary just right. But what if we add an outlier ...

Now the mean is too high and it doesn't seem to represent the average of the data correctly. The outlier drags the mean to its direction.
The mean also doesn't work nicely with skewed data. In situations the data is skewed, the mean doesn't give us the accurate central tendency location. As we said before, it happens because the skewness pulls the mean away from the representative values in the middle.
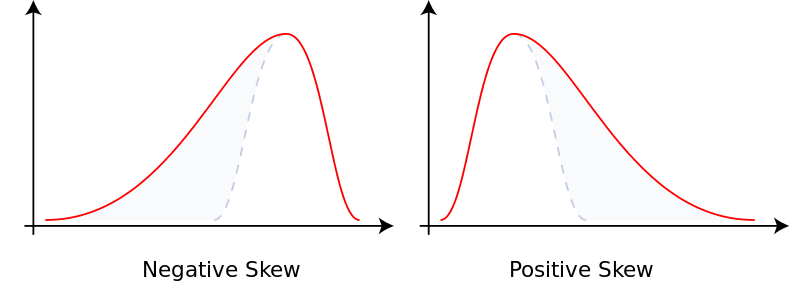
Skewness shows the degree of symmetry (-,+,0)
We can overcome these issues with the mean by paying more attention to its close colleague: the median.
Median
The median is the middle number in data. It divides the data set in two equal parts. There are some rules to follow:
- If the number of values in the data set is an odd number, then the median is the middle value:
- But if the number of terms is even, then the median is the average of the two terms in the middle:


Note: the median works only with ordered data. So sort first, then use the median. Because it is ordered, one half of the data lies below the median and the other half above the median.
In contrast to the mean, the median is more robust to outliers. We can see it on our previous example with yearly income:


The median stays stable even if we have a large outlier.
We also should use median and not rely on the mean in case our data is skewed:

Mode
The mode denotes the most frequently appearing value in the data set. If we look on the previous histogram, we can easily identify the mode by looking at the tallest bar:

In case of the normal distribution (where data is distributed symmetrically), the mean, the median and the mode are all the same. The measures of central tendency (mean, median, mode) display the most representative value in the data.

It's important to note that we can use the mean and the median only on numerical data. The mode, on the other hand, can be used even if we have nominal data in our data set. Note: nominal data focuses on depicting certain categories, so it represents categorical data. A usual example of nominal data would be gender: male and female, eye/hair color or nationality (American, German, etc..). Those are all limited number of groups.
Mid-Range
We previously named three major measures of central tendency: mean, median and mode. But one more measure for the central tendency which is also worth mentioning is the mid-range. The mid-range is a number which represents the average between the smallest value and the greatest value of the data. This number is called the mid-range. The formula for finding the mid-range is rather simple: we find the mean of the two values: one is the smallest and the other one is the greatest:
mid-range = min_val + max_val / 2
Summarizing mean, median and mode
use mean in cases where:
- the data is numerical
- the data has no outliers
- the goal is to find the most typical value of the data set
use median in cases where:
- the data is ordered
- the distribution (data) has outliers and is skewed
- the goal is to find the central values of the data set
use mode in cases where:
- the data is numerical or categorical
- the goal is to find the most frequent value of the data set
Read Part II and III next :)
Further recommended readings:
Introduction to Statistics Part II

