PCA
PCA is a statistical method which utilizes an orthogonal transformation. The lengths of vectors and the angles between those are defined through their inner product. An orthogonal transformation maintains vectors' lengths and angles between them.
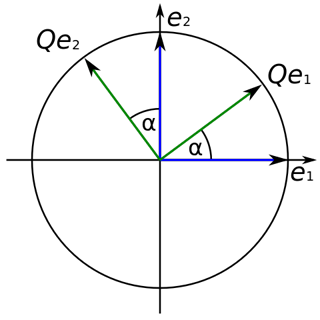
( Qe1, e1 ) = ( TQe1, Te1 ) -> ( Qe2, e2 )
An orthogonal transformation (which is a linear transformation) is used to transform some correlated variables into linearly uncorrelated variables. Those are called principal components. They are called uncorrelated because of the fact that e.g. the first principal component is uncorrelated to the second one and vice versa.
Each newly gained principal component is a linear combination, which we calculated from the original variables that exist in higher dimensions. Principal components show the direction of the most variation in data. Generally speaking, principal components are the lines of the largest variance. The main target of dimensionality reduction is to project the initial data on a line (or plane) of the largest variance.

The dots' spread is along the diagonal line. The maximum variance of the data lies between two endpoints of the horizontal line (1) as well as along the vertical line (2).

Let's turn it in a specific way ... We got new x, y axes. These new axis helps us to see the variation easier. Our data varies a lot more from left to right as up and down.
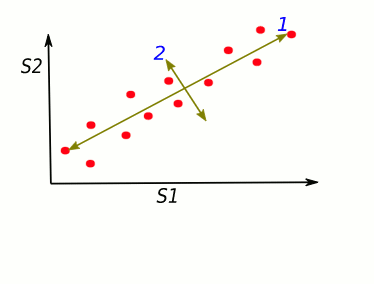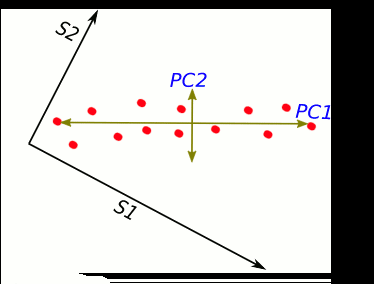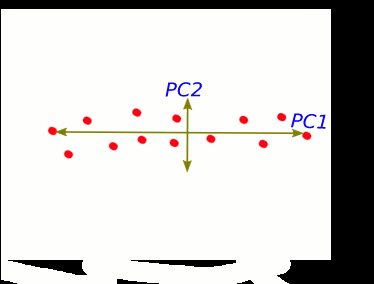
S1 and S2 stand for "sample 1" and "sample 2".
These two new axis that describe data variance are principal components.
This method allows us to gather principal components in a specific order:
- the first, and the most important principal component, demonstrates the maximum variance in the data.
- the second principal component describes the remaining variance in the data and is uncorrelated to the first principal component.
- the third principal component describes the remaining variance which was not described by the first two principal components and so on.
Because PCA transforms data into linearly uncorrelated variables (components), the variables (components) are uncorrelated between each other.
Maximum Variance: Sum of Squared Distances
As we shew before, our goal is to find principal components in a high dimensional data in order to reduce dimensions in this data. To find principal components, we have to find the maximum variance across the data. To find maximum variance in the data, we use the formula of the sum of squared distances (here SSD for short). To understand how SSD works, let's observe the PCA technique step by step:
For starters, lets plot some data on a graph and calculate the average measurement for the sample 1 and the sample 2 (here S1 and S2 accordingly)

With these average values, we can calculate the center of our data and shift the data in a way, so the center of the data is placed on the origin of the graph (0,0).

Now we will try to fit a line on this data: we start by drawing a random line that intersects the graph right in its origin. Then we rotate the line until the line fits the data as good as it can with the condition that the line still have to go through the origin. In the end, some line will fit best. Note: each data point on the graph is fixed as well as its distance from the graph's origin. That means, the distance from the point to the origin doesn't change, when the line tries to fit the data aka rotates.
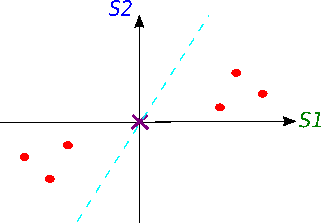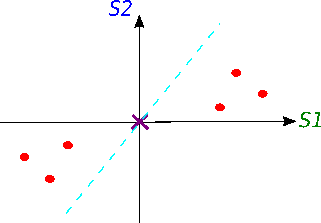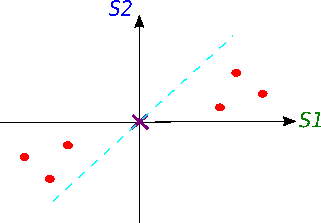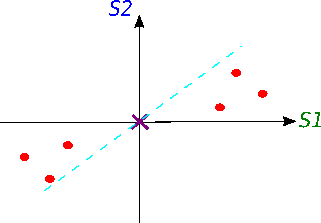
A good fit?
How do we know in the end that this final separating line fits the data the best way possible?
First of all, we already know that PCA projects data points onto the separating line. So, we can:
- either measure the distance from each data point to the separating line and find the line that minimizes these distances or ...
- ... PCA can find the line that maximizes the distances from the projected points to the origin

minimizing distances

maximizing distances
It is normally easier to calculate the second variant through a line that maximizes the distances from the projected points to the origin because PCA maximizes the sum of the squared distances from the projected points to the origin.

d12 + d22 + d32 + d42 + d52 + d62 = sum of squared distances ( SSD )
Note: We always want a line with the largest SSD .
We normalize our existing vectors in a way, so their length is one unit long. Such vectors are called singular vectors or eigenvectors. Eigenvectors have a characteristic that no matter what, they always stay at the origin. SSD is actually a scaling value or, in other words, it is a representation of eigenvalues. The root of a SSD is a singular value.
What will happen if you don't rotate the components?
The orthogonal rotation is essential for the correct PCA calculation. The rotation part maximizes the difference between variations captured by the principal components. The main objective of PCA is to chose less components than variables (data points). Those components can then describe the maximum variance in the data the best. Rotation only changes the coordinates of the points, the relative location of the components, on the other hand, doesn't undergo a change.
We will have to explain variance in the data by choosing a higher number of components (axis), if we don't apply the rotation of the components (axis). Therefore, the major PCA effect of dimensionality reduction diminishes.
PCA is realized on a covariance matrix. A covariance matrix is a matrix with some random elements in some position i and j. This position represents the covariance between the elements. Covariance is measured by the joint probability of two random elements.
Joint probability operates on dependent variables and calculates the probability of two events occurring together simultaneously. It's the probability of an event A occurring at the same time when an event B occurs.

If you've already read our article on T-Distributed Stochastic Neighbor Embedding also called t-SNE, you could ask a question: What are advantages and disadvantages of both methods? What are some differences between those?
First of all, we'll notice that both PCA and t-SNE are used for dimensionality reduction.
- To start with differences, t-SNE is a probabilistic technique, whereas PCA is not based on probabilities but more on pure math.
- PCA gives us a linear transformation for dimensionality reduction. We cannot say the same about t-SNE. T-SNE minimizes distance between the dataset in a non-linear way, for example by gradient descent.
- PCA is computed iteratively. That means, if we've already computed some n principle components and then decided to add a n+1 dimension, that will take only some more additional computation. Whereas, t-SNE computes the first n principal components and only then maps these n-dimensions to a 2D space, which means, we have to recompute everything each time we add a new dimension.
- PCA was initially invented in 1901 by Karl Pearson, as a counterpart to the principal axis theorem in mechanics. Later, in the 1930s the PCA method was independently developed further by Harold Hotelling. On the other hand, t-SNE is a relatively new method and was developed in 2008. You can take a look at the original paper: Visualizing Data using t-SNE
The Mathematics behind PCA

By adding constants and variables to the equation, like here: cy and dx, we can move our object (in this case a plane) in a 3D space. The same is also possible in multiple dimensions.

Suddenly, we got an ellipse and went from 3 dimensions to only 2 dimensions! Why does it happen?
Let's take another function x2 which is a parabola and looks like this:
Now, let's write it in this way: x2 = 1 which will be: x2 - 1 = 0 and we get:
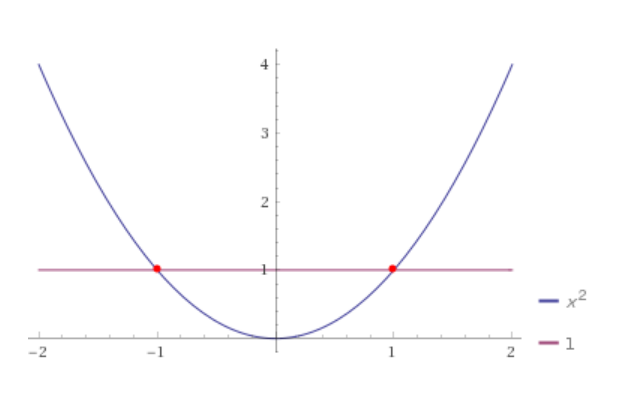
To mark it exactly, we have a number line now, aka we reduced the number of dimensions to only one:

In the end the two solutions for this function are: x = - 1 and x = 1. Putting everything not relevant aside, we can present the number line in the following way:

The same principles are applied to our equation above:

Note: an eigenvector is a special type of vector which stays on the original line and only gets scaled by some factor (scalar or also called eigenvalue)
In the last two steps we give our graph (object) some form and then we center it:
Step 5: give a form: a(x - x move)2 - b(y - ymove)2 - 1 = 0
Step 6: center it: a(x)2 - b(y)2 - 1 = 0
Conclusion
PCA is a linear dimensionality reduction method with the main goal to maximize variance and keep large paired distances: data points, which are more different, are placed far apart from each other. In PCA such procedure may cause poor visualization. It is especially difficult in cases, where we have to work with non-linear geometric structures, like for example ball, curve or cylinder. In such cases it is better to use t-SNE. T-SNE keeps small paired distances and PCA maintains large paired distances to maximize variance.
In PCA we can chose the components that would describe the maximum variance in our data set. In general, PCA tries to detect correlated dimensions in some set of variables (like e.g. BOW vectors) in a high dimensional data set and then merge some dimensions into one.
Further recommended readings:

