Introduction to Reinforcement Learning
What is Reinforcement Learning?
Reinforcement Learning (RL) belongs to the family of Machine Learning techniques that are more close to the field of Artificial Intelligence. First of all let's go through the first (and not the last :D ) portion of some important terminology in RL:
agent - a model which moves in an environment and tries to perform the best action in order to maximize the reward.
environment - the "world" where the agent interacts; environments can be provided with a model (model-based) or be model-free.
actions (A) - transition steps the agent takes to move within an environment. Every action returns a reward.
reward (R) - a response value to an action. The goal is to maximize the total reward the agent receives in one episode (all the states in between from the initial to the terminal state, sometimes also called trajectory).
policy (π) - describes how the agent acts. A policy is a function that returns the probability of taking an action a in a state s, so it is a probability distribution over actions given states. This is the strategy of the agent.
The main goal in Reinforcement Learning (RL) is to learn an optimal policy. An optimal policy describes how to act in order to maximize the reward in every state. Once more, policy π is a special mapping (=function) from states to optimal actions in these states: π(s) ∊ A(s) so that the agent always knows what to do.
The policy basically tells us how much reward the agent can get in each separate state.

We will first start from some broader concepts to get a bigger picture and afterwards will narrow down the idea to more and more specific methods.
Modelfree vs. Modelbased Approaches
There are two main methods to work with RL models:
- model-based methods: algorithmic methods which apply the transition probability table and the reward function from some Markov Decision Process (MDP). In RL a Markov Decision Process (MDP) represents the problem we seek to solve.
- model-free methods: we will discuss the model-free methods in Part II of these series but for now, a model-free approach uses no transition probability table and no reward function. The transition table and the reward function are sometimes called the "model" of the environment (MDP), so the name "model-free".
Markov Decision/Reward Process (MDP/MRP)
To fully understand Markov Decision Process (MDP) let's look at the so called Markov Property first:
The Markov Property is the memoryless property of some random process. All right and what does it mean?
Some random process incorporates the Markov property if the conditional probability of future states depends solely on the present state, hence the name "memoryless property". There is no past ... so essentially the Markov property omits all the events from the past.
P(future | present, past )

A process which satisfies this property is called a Markov process.
In the world of RL (and ML in general) it is easy to get overwhelmed with a lot of different terminology and the lingo. So let's differentiate between the following terms:
Markov Process is a tuple of the form (S, P) wherre S - a finite set of States and P - state transition Probability matrix.
Markov Reward Process (MRP) is a tuple (S, P, R, γ) where R - Reward function, γ - discounting factor (more on γ later on). MRP describes no environment (as e.x. a MDP does). A MRP tells us how much reward the agent could accumulate after passing an episode (=a sequence of states). The Reward function R is defined as:
Rstate = E[Rnext state | Scurrent stae ]
Markov Decision Process (MDP) is a tuple (S, P, R, γ, A) where a ∊ A - Action taken in a state s ∊ S.
The dependency between MDP and MRP is the following: in RL a MRP is needed when we try to fix a policy π for a MDP.
From now on we will primarily concentrate more on MDPs and on MRPs.
Markov Decision Process (MDP) is a discrete time, random control process. It describes an environment for RL, which is fully observable, hence model-based. A fully observable environment always provides the agent with all the existing states, so the agent has full knowledge of the environment. Control in RL means the approximation of the optimal policy π, also called policy improvement (more details later on).
In essence we can think of an MDP as of a mathematical formulation of an RL problem we are trying to find solution for.
A quick summary : an MDP sets up an environment for a RL problem. In an MDP the environment is fully observable. Practically all RL problems can be presented as MDPs.
As we talked about the reward function, let's generalize this idea to the so called return Gt where the subscript t is the current time step:

where R is our Reward function from above and γ is the discount factor.
The role of γ
The γ (=gamma discount factor) controls how much the agent should care about immediate or future rewards. The γ factor lies in the range [0;1] where if for example γ = 1, then the agent always considers the rewards from far away in the sequence (=the agent is "far-sighted"). If γ = 0, then the agent only cares about the first reward (=the agent is "short-sighted").
γ is called "discount factor" because it discounts the value of a state as the agent goes away from the goal. The agent follows the path (=sequence of states) with maximum values it can get in a state.
We can also think about the γ factor as when it has a low value (near to 0), the agent has short term thinking, whereas if γ is high (near to 1), the agent has long term thinking.
Value Function
The value function is a useful tool to gain the value of being in some state s. What is this value? This value shows possible future rewards that could be received by the agent from being in this state s.
The value function can be seen as cashing of useful information we can use later on and comes in two flavors:
- the "normal" state value function and
- the state-action value function.
For a given policy π the state value function is defined as:

For a given policy π the state-action value function is defined as:

In the above equation we focus on a particular action and its return in the state s.
Both equations give the expected discounted return G t starting from the state s following the policy π .
Bellman Equation
The backbone of many RL algorithms lies in the Bellman Equation. Let's recall once more: the goal of RL is to choose the optimal action which will maximize the long-term expected reward given the current state the agent is in.
The Bellman Equation helps us in finding the answer to the question: given the state the agent is currently in, if the agent takes the best possible action at the current and each further step, what long-term reward will the agent get?

We can also write this equation down as a linear equation system in matrix notation :

Using the Bellman Equation we can easily find the value of a state.
Consider an example MRP :
Imagine that we have an agent that tries to explore the environment around it and to gather maximum reward for its actions.
We have the following scenario : the agent is on a small detached lonely island which is the start state. Because nothing ever happens on this island the agent "gets bored" and receives the negative reward for being in this state (-2). The goal of the agent is to explore the environment and land on the mainland which is the terminal state with the reward (0). The agent builds a boat and tries to reach the mainland - so we have a state "boat" with the reward (-1).

Let's say that there is a 0.5 probability that the agent will still stay on the island though it's bored, 0.4 probability that the agent gets on the boat and starts the dangerous journey and 0.1. probability that the agent might be directly taken by some magical accident to the mainland without doing anything. Once the agent decides to get on the boat with 0.5 probability the agent stays on the boat, with 0.2 probability the agent returns back to the island and with 0.3 probability the agent successfully reaches the mainland and goes to a party :D .

Now we build a transition probability table for the states i - island, b - boat, m - mainland:
| Transition Probability Table ( = P ) | ||||
|---|---|---|---|---|
| to | ||||
| i | b | m | ||
| from | i | 0.5 | 0.4 | 0.1 |
| b | 0.2 | 0.5 | 0.3 | |
| m | 0 | 0 | 0 | |
Here we can apply the Bellman Equation written in the matrix notation we already presented above:
(I - γ P) * V = R where we assume γ = 1 :

Solving this system of linear equations will give us the values for each of our three states (island, boat, mainland).
Dynamic Programming: What Is It?
Dynamic Programming (DP) is an approach to solve complex problems consisting of multiple components. The approach breaks a bigger problem in some smaller subproblems. Then we try to solve those smaller subproblems and in the end we generate an overall solution.
In the context of DP we have to clear up some terminology (again :D):
- prediction: or policy evaluation, at this step we compute the state-value function Vπ for a policy π . The input of a prediction step might be an MDP or also an MRP. The output is a value function Vπ .
- control: policy improvement, here we try to approximate optimal policies. The input is an MDP and the output is the optimal policy π* and the optimal value function V* .
Both control and prediction fall into the category of Planning in DP.
In order to be able to use DP, our problem has to satisfy the following two criteria:
- it is possible to decompose the problem into smaller parts
- we can solve subproblems recursively by caching the information
MDPs meet both these properties as the Bellman equation gives a recursive decomposition and the value function stores solutions.
Dynamic Programming (DP) belongs to the family of model-based approaches. DP assumes complete knowledge of the MDP, so we have a transition probability table and the reward function. We will now go through two DP algorithms that help to find the optimal policy, namely: policy iteration and value iteration. With these two algorithms we are able to find the best policy π .
Policy Iteration
Let's start with an example and return to our already mentioned island agent. The agent can now perform two certain actions, namely:
- change position
- learn to fly
Moreover, the agent changes its position with probability 0.8 if it is on the island or on the boat, else it stays where it was with probability 0.2. With a very small probability 0.1 the agent learns how to fly and flies to the goal mainland directly from the island or from the boat. With a higher probability 0.9 the agent doesn't learn to fly and stays put on the island or on the boat.
change position
learn to fly

Now we will apply policy iteration to find out the optimal policy π and the state values V(s) of: island - i , boat - b and mainland - m. For simplicity we assume that the initial policy π0 has the action learn to fly in both states.
Step 1 policy evaluation:
For the policy evaluation step we will use the simplified Bellman equation for a fixed policy πfly .

where s is the current state and s' is the new state the agent moves in. We take γ = 1, so we take all the rewards into account and basically have no discounting of rewards.
Consulting the MDP from above we conclude:

Analogously we compute:
Vb = -1 + 0.1*Vm + 0.9*Vb
Vm = 0
Now we can plug in Vm = 0 into the first equations and get Vb = -10 and Vi = -20
Step 2 policy improvement:
In this step we use the Bellman Optimality Equation for finding the action that maximizes the value function for every state.

Because R and γ are independent of the action the agent takes and therefore they don't influence the maximization problem, we can simplify the above equation as follows:

We simply neglected the R and gamma γ terms.
Let's denote the Σ s' P(s'| s,a)*V(s') part as T(state, action) and we get:

Now we have to choose the maximum value. Because T(i, fly) < T(i, change) = -18 < -12 the action change is preferred in state island. However in the state boat, T(b, change) < T(b, fly) = -18 < -9, so the action fly is preferred in state boat.
We repeat the steps 1 and 2 until the new proposed actions stay unchanged.
Again let's summarize the whole algorithm systematically:
- start with initializing a random policy.
- policy evaluation step (=prediction): find the value function V(s) of this policy by applying the Bellman equation.
- policy improvement step (=control): find a new improved policy, take the action that maximizes the value function V(s) for each state.
- repeat the step 1 and 2 until the variable unchanged is True.
Value Iteration
With value iteration we can go further and join both steps. We update the Bellman Optimality Equation directly.
The algorithm updates the policy based simply on the Bellman optimality equation (= the control step only):
- start with some random Value function V(s).
- policy improvement step (=control): find a new improved optimal value function V*.
- repeat the step 2 until reaching the optimal value function.
Policy Iteration vs. Value Iteration
Down below you will find the pseudocode for the two algorithms. See for yourself and compare:
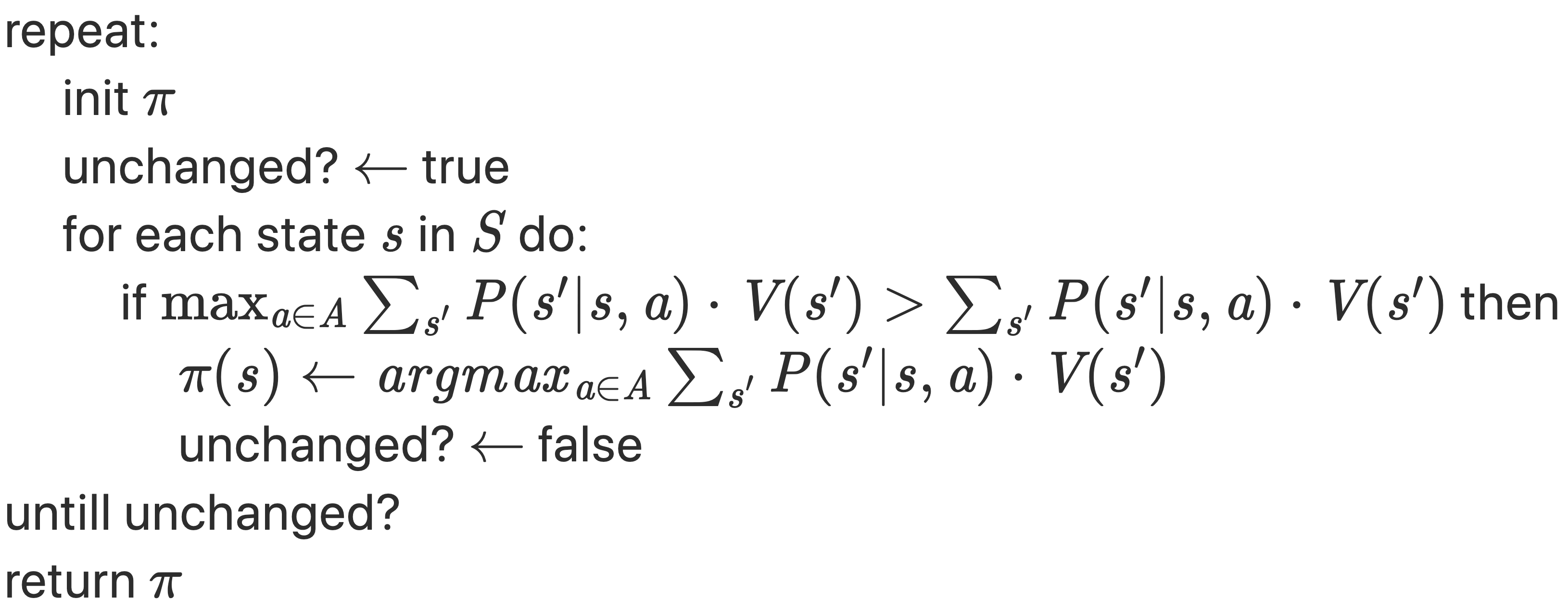
policy iteration
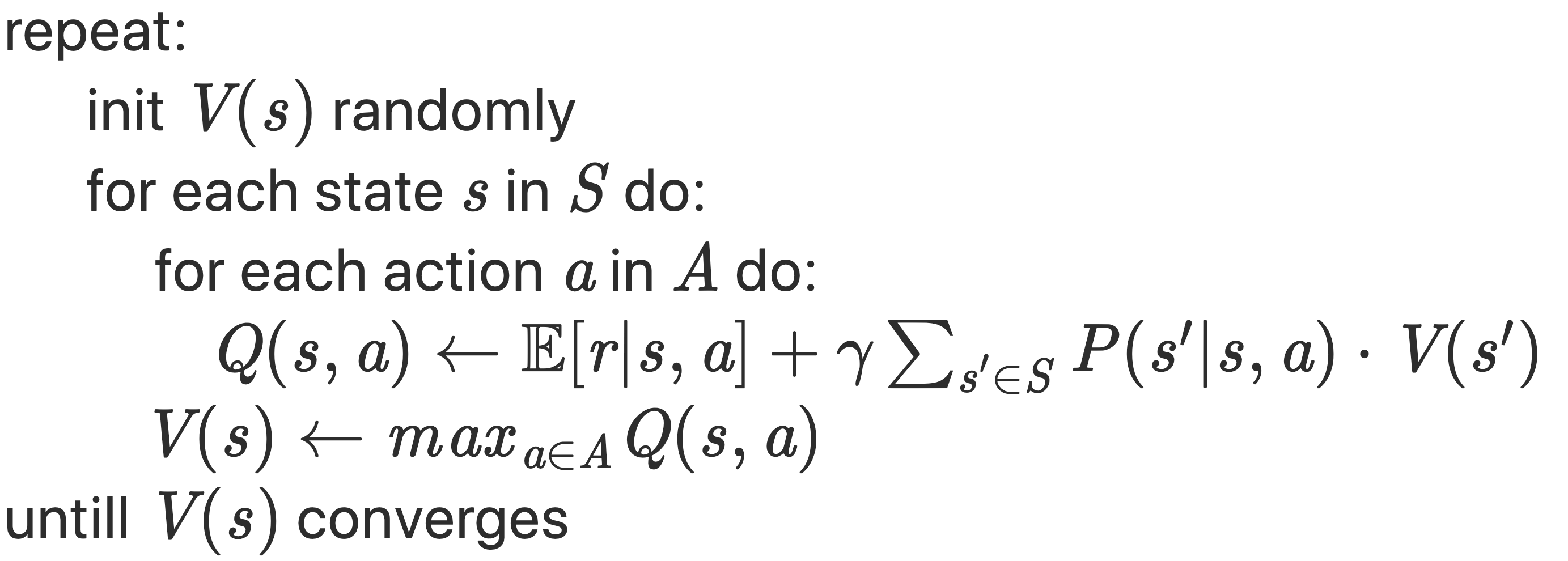
value iteration
Conclusion on Policy/Value Iteration
The policy iteration algorithm helps us to look for the optimal policy. The exact state values are not that relevant if one action is clearly the optimal one. Principally, there are two major steps: 1. policy evaluation and 2. policy improvement. Within the step 2 (policy improvement) the algorithm acts "greedily" because it takes the maximum over all the sate values.
With value iteration we can directly jump to the control step and update the value function using the Bellman optimality equation. It saves us some memory and backs up on more recent versions of the value function
The prior goal of both policy iteration and value iteration is to figure out the optimal policy for the agent to follow. The new policy has to be a strict improvement over the old one. Both policy iteration and value iteration belong to the family of Dynamic Programming methods.
Further recommended readings:
Part II : Model-Free Reinforcement Learning
Part III : Value Function Approximation
Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto
Python code for Artificial Intelligence: Foundations of Computational Agents

