SVM
SVM Introduction: problem stated, problem solved
Let's imagine the situation where we have some medical data samples. With these samples we want to predict whether a patient is ill or not. We plot the data and try to find some value which serves as a threshold. If we go above the threshold, then the prediction is the patient is ill and if under the threshold, then the prediction is the patient is not ill. How about this one:

All right, seems correctly classified at the first glance. Now a new value from another patient comes in and we also want to classify it:

We don't really know now whether the patient is ill or not, the new data point is classified as not ill, but it is definitely closer to the ill class.
What we can do is following: we only focus on data values which lies on the side edges. For later, we call those "edge"-data values - support vectors. When we have our support vectors, we draw a line right in the middle from both support vectors (data points) - this is our new, better threshold. Now if the new data point comes in, it will be correctly classified.


More concrete about SVM
From the visual example above we can conclude that with SVM our goal is to find a line (or a hyperplane) in some n-dimensional space, where n is the number of dimensions. For a 2-dimensional space we use a line as a separator and in higher dimensional spaces we use a hyperplane. In this article we will mostly use the line as a term for separator, so we use n=2 dimensions. Furthermore, those dimensions (n) are just the number of features (input values).


The line, we search for, has to divide the data points in two groups the best way possible. This "best way" can be found by maximizing the margin , so the line distinguishes the data point most clearly. Let's see why.
Here we have some data points which are placed in two groups:

Which line does separate those data groups the best? There may be an infinite number of lines ...
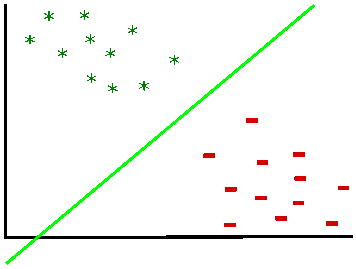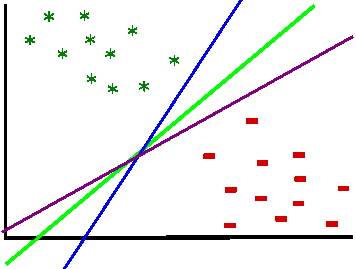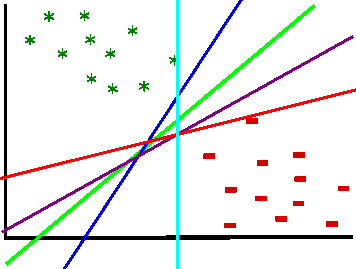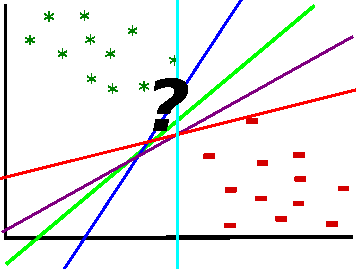

Well, as we saw in the introduction, the ideal line is the line which lies right in the middle of the biggest separating margin. So, we want to maximize the margin and draw a separating line in the middle. Margin is basically what builds the decision boundary, it is the distance from a data point which is placed closest to the line, till the beginning of that line. A margin can be seen as the maximum width that separates the support vectors of two classes:
When we maximize the margin, we provide reinforcement to the SVM model in a way that it classifies other data points more confidently. This reinforcement part is also one of the features of the supervised learning.


Support vectors are the data points which "support" the margin. Only they are important for finding the decision boundary. If we remove those points, we will change the position of the decision boundary. Support vectors lie on the beginning of the margin boundary and are used to maximize it. Data points that lie on the one or the other side of the decision boundary can be assigned to one or the other class.
The SVM algorithm looks only at those support vectors to compute the margin. From there it is able to assign the data from one side of the decision boundary to one class and the data from the other side of the decision boundary to the other class.
Why maximizing the margin?
Can't we just take some line that separates the data in two parts? Maybe somewhere in the middle? Well ... Nope, if we do so, we lose let's call it the "confidence"-measure in out model. Each distance from a data point to some separating line corresponds to the "confidence" of the prediction for that point's group. By maximizing the margin (the decision boundary), we maximize the level of confidence for our prediction for a data point. In other words, data points that lie near the separating line stay for uncertain classification decisions. That means, there is nearly 50 % chance this point can belong to the "other side" - to the other class. By maximizing the margin we make sure, that the closest point to the separating line which lies on a margin boundary, is still relatively far away from the line itself, thus increasing the probability that this point was classified correctly:

Defining the hyperplane
We can determine the separating line - a hyperplane, by using the so called weight vector (w⃗) and the intercept (b) which is sometimes referred to as the bias. The bias term represents the rate of how good a machine learning algorithm can show true correlations between the data points. The w⃗ vector is perpendicular to the hyperplane and logically the hyperplane is perpendicular to the weight vector as well.

A perpendicular line crosses the other line at right angles 90 °
In order to select the right line (hyperplane), we need the intercept b. The intercept which is often presented as a constant is some point at which the weight vector crosses the line (hyperplane).

Let's take a set of training data points S = { (x⃗ i , y i) } where x⃗ is a vector representing each data point at the index i and y is a corresponding correct label to the data point x⃗ i . In SVM the two data groups we want to classify the data points into, are given as 1 and -1 . So the 1 stays for one class and -1 for the other class.

where:
- w⃗ is a perpendicular weight vector
- x⃗ i is a vector sample from the training set
- b is the intercept (sometimes called "the bias term")
- >= +1 and <= -1 are the threshold values, which define at which time one data point should be classified in the respective group
We can also present the formula above in a more concise way :

To conclude, the equation: ( w⃗ * x⃗ i ) + b is the predictor for one sample xi
SVM belongs to the class of discriminative models. Discriminative means: the algorithm models a decision boundary between classes.
In the python library sklearn we can find a ready implementation of SVM:
from sklearn.svm import SVC The Kernel Trick
The kernel is a group of mathematical functions. It transforms data into a different form.
The main idea of the kernel function is to bring data into higher dimensions. Why do we need it? Imagine that we have a data set which is not linearly separable, so we cannot draw a line between two classes.


With the kernel trick we can separate data that is not linearly separable by bringing it into higher dimensions.


There exist different kernel functions: linear/nonlinear kernel, polynomial kernel, sigmoid kernel, exponential kernel ...
Linear Kernel:
The linear kernel predicts the classification for a new data point in 2-dimensional space. It does so by calculating the dot product of the input and every support vector:
f(input) = Σ (weighti * dot(input, support_veci)) + bias(0)
Polynomial Kernel:
f(input, support_veci) = 1 + Σ(input * support_veci)n
where n is the number of dimensions.
In contrast to the linear kernels, polynomial kernels are used to figure out the separating hyperplane in higher dimensions.
Again, using the sklearn library makes our life easier:
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
classifier = SVC(kernel='linear')
classifier.fit(x_train,y_train)
y_pred = classifier.predict(x_test)
print(accuracy_score(y_test,y_pred))Conclusion
Support Vector Machines is a powerful algorithm for classification tasks. It is widely used in image classification, text categorization, hand-written character recognition, as well as in face recognition systems.
Further recommended readings:

