Gradient Descent
Gradient is the derivative of the loss function. Derivative is the instantaneous rate of change or the amount by which a function is changing at one particular point on the function curve. Gradient is basically a slope of the tangent line at some point on a graph. And a slope is a rate of a predicted increase or decrease. The value of a slope is a scalar (singular value). To sum up, if we can determine this tangent line, we could calculate the right direction we should move to reach the minimum of the function. Moreover, the tangent line demonstrates us how steep the slope is.

It is possible to find the minimum of some function by computing its derivative (aka slope).
We can find the minimum of a function if we move in the direction of steepest descent step by step. This steepest descent is determined by the negative of the gradient.

Gradient Descent is necessary to update model's parameters. These parameters refer to coefficients if we talk about linear regression and weights in context of Neural Networks.
Gradient Descent's main goal
The prior task of Gradient Descent is to minimize a loss function (also called cost or error) for an objective. The loss function shows how wrong or right the performance of a machine learning algorithm is. Gradient Descent iteratively adjusts parameters of the Neural Network to gradually find the best combinations of weights and biases to minimize the loss function.
A bias is an intercept of a function, a point where a line crosses some of the axis.

Loss Function (also cost or error function):

Gradient Descent: The Algorithmic Thinking
One general version of the Gradient Descent algorithm would look like that:
- guess an initial solution
- iteratively step (descent) in a direction towards better solution
(function's minimum)
- if the solution is still not optimal, repeat 2
Another way of thinking about Gradient Descent would be:
Let's say we have a question: What is the smallest Y value?
We have a function X 2 :
- We calculate the minimum value of it (here the Y value is the smallest)
- We find the derivative of it: 2x
- We use that derivative to calculate gradient at a given point
- We repeat till convergence (till finding the local minimum of the function)

Let's look precisely at the picture above: the function has the form Y = X 2. This represents a parabola in a coordinate system. If we aim to minimize the function shown above, we want to find the value of X, which gives us the lowest value of Y which is the dark dot.
Power Rule
How did we actually calculated 2x from X 2 ? Well, X 2 is the calculated derivative of the variable X raised to the power of some present constant (in this case 2).

For example, what is the derivative of the function: f(x) = 2x 4 ? It's 8x 3
Summing up: Traditional Gradient Descent
To sum everything up, the traditional Gradient Descent procedure looks like this:
- take the derivative (slope of the function) of the loss function for each parameter in it
- pick random values for these parameters
- plug the parameters values into the derivative
- calculate the step size: Step Size = Slope * Learning Rate (also called Gradient Step)
- Calculate a new parameter: New Parameter = Old Parameter - Step Size
- repeat 3
Learning Rate
In order to know how we move in the direction of the steepest descent, we need a learning rate. Learning rate determines how fast we want to update the weights in our model, which means we state how fast our model learns. Learning rate is a scalar value. During each iteration the Gradient Descent algorithm multiplies the learning rate by the slope (gradient) of a function. The product is called the Gradient Step.
If we set learning rate to high, the model will skip the optimal solution. If we set learning rate to small, the model will need too many iterations to converge.

Learning rate controls how fast the point on the graph should approach the minimum value of the curve. You can train your new knowledge on learning rate by doing some interactive exercises .
Back to Gradient Descent
Traditional GD computes the gradients of the loss function with respect to the parameters of the whole data set for a certain number of epochs (number of complete iterations through the training data set). If we need to calculate gradient of the entire data set (which may consist of millions of data points) in a single update, the optimization may work slowly and even the single iteration can take a long while. Besides, if we have enormous amount of data initially there is a chance of redundant data that doesn't contain much useful information and yet is in the analyzed data set and has to be worked with.

Traditional Gradient Descent:


The problem is: we have to compute the gradient of the loss function by summing up the loss of each sample. And we can have millions of them.
To overcome the slow optimization, use Stochastic Gradient Descent.
Stochastic Gradient Descent (SGD)
SGD performs parameter update for each instance (data training example and label) one at a time (batch size = 1). SGD implements more frequent updates with high variance. It causes the objective function to vary more intensely, which helps to find more optimal local minima. With every iteration, we need to shuffle the training set (in order to create a pseudo randomness) and pick a training example at random. "Stochastic" signifies that one example, which makes up each batch, gets selected at random.

The problem with SGD is: since we're using one training instance at a time, the path to the local minimum is going to be noisy, which means the path would be more random.
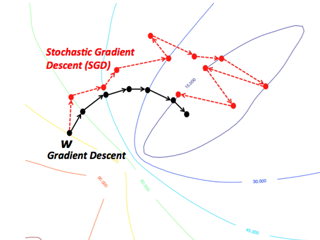
An improvement would be a Mini Batch Stochastic Gradient Descent, where we can decide the size of a batch with training examples to perform an update upon.
Mini Batch Gradient Descent:
1 < Batch Size < Size of the entire training set
Mini-batch SGD is good for noise reduction in SGD, nevertheless is still more efficient than the full batch version because it is more effective to compute the loss function on a mini batch SGD than on the entire training data.
Popular batch sizes are: 32, 64, 128 samples.
The Drawback of Gradient Descent
One major problem in Gradient based models and backpropagation is called "vanishing gradient". As we go further and calculate our gradient steps, the value of a gradient will consequently "vanish". That means, the gradient becomes vanishingly small, which blocks the weights from changing its value. Thus, if weights stay unchanged, the neural network stops to learn.
There are more Gradient Descent based optimization strategies. You can have a look at some of them at Google's TensorFlow.

