Logistic Regression
Precisely speaking, a classification task is a task of predicting a discrete class label.
Logistic regression is sometimes called (as already mentioned) Logit, Maximum Entropy Classifier or Log Odds and it is used when the outcome (response variable) is categorical in its nature, e.g.: yes/no, true/false, 1/0, red/green/blue.
The name "Logistic Regression" comes from a similar technique used in Linear Regression. Logistic regression is sometimes called Logit because of the Logit function that is used in its method of classification. Thus the name "Logistic" was taken from this Logit function.
The Logistic function and the Logit :
The logit function is used to predict the occurrence probability of some binary event. A logit function is just the inverse of the logistic function. We can apply the natural logit function to convert the odds logarithm into a probability. So keep the Logistic function separate from the Logit.
the logit :
f(x) = log (x / (1 - x))
the plot of the logit function:
The Logistic function (also "the standard logistic sigmoid function") has an explicit S-shape and is presented in the following picture:
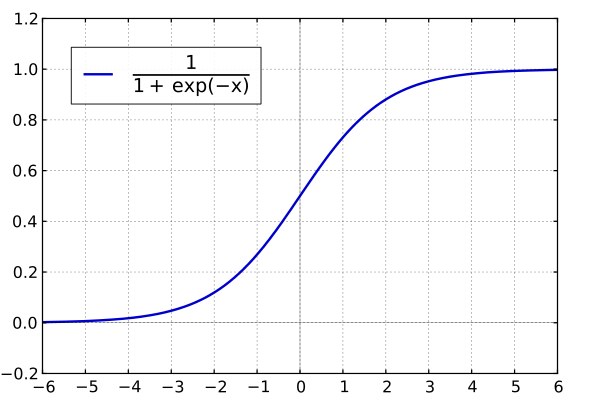
The Logistic function is sometimes called the logistic sigmoid function. Logistic sigmoid is one of the activation functions. Logistic sigmoid takes any number and outputs a probability for it between 0 and 1. Furthermore, the logistic function could be referred to as the expit function.
If you are looking for an easy implementation of the logistic function and the logit function, you can use the scipy library in python:
from scipy.special import expit, logit
Back to Logistic Regression
Logistic regression belongs to the class of discriminative models. A discriminative model represents a decision boundary between the classes and is a model of conditional probability:
p(x|y)
Decision Boundary: Linear

Decision Boundary: Non-Linear

There are also some other models which belong to the discriminative class. Some of them are: K-Nearest Neighbors (KNN), Maximum Entropy, Support Vector Machines (SVM) and Neural Networks.
Logistic regression is a special case of linear regression. In contrast to logistic regression, a linear regression outcome is continuous in its nature, e.g.: height, weights, hours, price on the stock market, etc. and not discrete as in Logistic Regression
Logistic Regression & Linear Regression. Differences
Logistic Regression Equation looks like:
Y = ex + e-x
Linear Regression Equation looks like:
Y = mX + C
The Ordinary Logistic regression needs the dependent variable to be of two or more particular categories. Binary or not ordinary logistic regression has dependent variable with only two categories.
Linear regression needs the dependent variable to be continuous that means no categories or groups are allowed (Note: a dependent variable is a variable that is being measured in an experiment. The dependent variable changes as a result to changes in the independent variable, e.g the person's height at different ages).
Logistic regression is based on Maximum Likelihood Estimation which means that we choose coefficients in a way that it maximizes the probability of Y given X (Y|X). This is also called likelihood.
Linear regression, on the other hand, is based on Least Square Estimation. The concept of LSE is that we choose coefficients in a way that it minimizes the Sum of the Squared Distances of each observed outcome. (Note: Sum of the Squared Distances means that we sum up all of the squared distances from the boundary (separating line in a Cartesian vector space) to each individual point. We normally would want a line with the largest sum of squared distances because that means that the line separated the data point the best)
Fitting the line to the data: Linear Regression vs. Logistic Regression


Maximum Likelihood Estimation
Logistic Regression makes use of Maximum Likelihood. Maximum Likelihood Estimation ( MLE ) is a widely used statistical method. It estimates the parameters of some probability distribution: MLE finds the values of the model's parameters which make the known likelihood distribution a maximum. Or in other words, MLE maximizes the likelihood (a likelihood function), in a way that the observed data samples are most expected to happen under the presumed statistical model.
L (w*, b*) = maxw,b L(w, b)
Parameters
We noticed before that MLE is a parameter estimation function. That means, MLE finds the values for the parameters. What are parameters then? Previously, we mentioned the linear regression equation: y = mX + c . As an example, the variable X might stand for expenses or investments in business and y could represent the generated income. Then m and c are the two model's parameters, that MLE seeks to determine.
So, parameters are important for the model sketching.
Another short algorithmic example of MLE :
- as an example, you pick some weight scaled probability of an obese person
- use that observation to compute the likelihood of observing a non-obese person with the same weight
- take the likelihood of observing this person
- do that for all people in the data set
- multiply all these likelihoods together. This is the likelihood of the data with the logistic regression line
- shift the line and compute a new likelihood of the data
- keep on shifting the line until you can select the curve with the maximum likelihood
To recap, we said that Maximum Likelihood tries to maximize the likelihood through parameter estimation. When the parameters fit good, then the data, that we want to have in the end, will be outputted. That is why, it is a very popular technique for parameter estimation. MLE will literally give you the parameters which suit your model the best.
Another crucial part to understand Maximum Likelihood Estimation is that we have to have a good idea of differentiation from calculus. It is a mathematical method which helps us to find maxima and minima of a function. To find the MLE values for some parameters we can apply the following algorithm:
- determine the derivative of the function
- set the derivative of the function to zero
- rearrange the equation in a way that the parameter of interest is the subject of the equation
To learn more about derivatives and partial derivatives, read Partial Derivatives and The Jacobian Matrix .
Summing up
Logistic Regression (like linear regression) is able to work not only with continuous data (e.g. age, weight) but also with discrete data (e.g. blood type).
Logistic Regression describes the relationship between a categorical dependent variable and one or more independent variables: logistic regression calculates probabilities with the help of a logistic function, which is often called logistic sigmoid function.
Further recommended readings:
Classification with Naive Bayes

