Word Embeddings
We can list some of Skip Gram model's negative sides:
- the model tends to become a very large neural network which means: the larger the neural network, the slower the update of gradient descent is, which means the learning is slow.
- a big neural network has a big amount of weights, so more data for tuning and avoiding overfitting is needed.
- if we have millions of weights (k) and billions of training samples (n), we get k*n which produces a large outcome.
How can we overcome those obstacles?
- treat common words/phrases as a "single word", so we reduce the number of samples.
- use subsampling for frequent words
- use negative sampling
- use hierarchical softmax
We can:
Subsampling
We choose the words which are the most frequent ones and delete them. The probability that those chosen frequent words are not relevant stop words (words like: "the", "a", "for", "and") is very high. So these words don't contribute to the meaning much and appear in almost each sentence get deleted, which reduces the number of not useful training samples.

Negative Sampling
As we said before neural networks tend to have a big amount of weights. Those weights need to get updated by every one of millions training samples, which makes the computation time consuming. Negative Sampling, as a technique, that modifies only a small percentage of the weights, not all of them, which eases the computation and the weights update.
Some "negative words" are chosen, those words are called "negative samples". We want our network to output 0 for those negative samples, so we choose the samples (words), which are less probable to appear together with the output words. So we have some word pairs which are unlikely to appear together. Those are our negative samples.
We can also choose our negative samples using the technique called unigram distribution, where more frequent words are more likely to be chosen as negative samples, meaning that the probability of choosing a word as a negative sample is related to its frequency. Because more frequent words tend to contribute less meaning, so we want the network to output 0 for them.
Hierarchical Softmax
First of all: What is softmax?
Softmax is a popular activation function. It is suited for multi-class logistic regression problem as well as for binary classification tasks. The softmax output is a probability distribution (or categorical distribution). The probability results of softmax (a vector) show what class is more likely to be chosen as a correct one. The singular probabilities in the softmax output vector must sum up to 1.
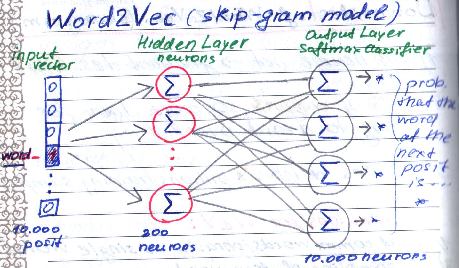
There is no activation function used on the hidden layer neurons and the output neurons use the softmax activation function.
An advantage of softmax at the output layer is that we can easily interpret the output of the neural network (a probability value between 0 and 1 for each class).
The problem with softmax is: it is computationally expensive as it sums over all samples.
The formula looks like this:

Now we know what a Softmax Function is. So, what is then
Hierarchical Softmax?
Hierarchical softmax is an optimization of the normal softmax. As we said before, the standard softmax has a time complexity problem that it sums over all given samples, which increases the computation. In hierarchical softmax we only need to update the parameters of the present training example. Less updates means in this case that the next training sample can be worked on sooner, so the processing time reduces as well.
Hierarchical softmax works different with conditional distributions: the parameter number with a single depended variable is proportional to the log of the data set samples in total. Hierarchical softmax is implemented using binary tree.
The Hierarchical Softmax Formula: O(V)--> O(Log V)
Summary
In this two part article you've learned about representing words as vectors, word embeddings, n-grams and the Word2Vec Model. In Word2Vec there are two submodels called Continuous Bag-of-Words (CBOW) and Skip Gram (SG). Now you know what optimizations techniques for SG exist (Subsampling, Negative Sampling, Hierarchical Softmax) and what are their consepts.

