Activation Functions
What are Neural Networks?
Shortly speaking, neural networks are algorithmic procedures, the structure of which relatively reminds our human brain. Those algorithms are architectured in a way, so that they can remember and even recognize certain patterns. These patterns, the neural nets recognize, are only numbers. Those numbers are enclosed in vectors. No matter what kind of data we have (images, text, sound, etc...), it must be converted into a numerical vector representation.
We use neural networks to cluster and classify our real-world data. We can think of them as a clustering or classification algorithm to manage and analyze information flows.
Neural Networks consist of layers. Layers consist of "neurons".
What is a neuron in Neural Networks?
An artificial neuron computes the weighted sum of its input, then it adds a bias:
N = Σ(input * weight) + bias
After the computation, the neuron decides whether to "fire" or not, or to activate itself or not. The value of a neuron may be any number from -infinity to +infinity. The neuron doesn't know the necessary boundary for its values - it doesn't really know when to "fire" and when not.
How the neuron decides?
We add an activation function for this decision. We now can check the N (neuron's) value with the activation function and see, whether the neuron should be "activated" or not.
Use a linear function?
What if we use a normal linear function as an activation function?
For example, we would use a linear function like that: L = yx ? This is a straight line activation function. In this case the output of such linear function is some numerical range. That means, it is not a binary activation. If you know the Gradient Descent optimization algorithm, you can also notice that the derivative of this linear function is constant.
But the bigger problem is: imagine some connected layers. Each layer has its own activation function, in our case we chose a linear function as an activation function. That activated output, based on a linear function, from one layer goes straight as input into another layer. The weighted sum is calculated and the output would be again based on another linear function. All in all, that indicates, no matter how many layers we add, the neural network will still behave like a single layer network because the sum of all linear layers gives another linear function. So it stays linear no matter what.
How do we bring in non-linearity?
We need non-linearity to solve more complex problems, in cases where the relationship between variables is not static or directly proportional to the input, but instead is dynamic and differ from time to time. In sales for example, per unit cost may decrease instead of staying constant as the output increases.
We can use non-linear activation functions:
Sigmoid Function

the range of the non-linear function sigmoid is [0;1] , that means we can easily calculate probability values and, unlike with the linear function, we now have a boundary.
The sigmoid function is frequently used for binary classification.
If you noticed, the function contains the constant e (more on e here) and e is the easiest function to get the derivative from.
The intercept of the function lies at 0.5, which is also beneficial for calculation probabilities when we have 50/50 chance of something or when we have sigmoid(0).
And finally, the sigmoid function is non-linear (non-linear curve), so it solves the problem mentioned previously: each combination of linear function is again a linear function.
Implementation of the Sigmoid Function
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(num):
return 1 / (1 + np.exp(-num))
num_seq = np.linspace(-5, 5, 100) #'np.linspace' creates evenly spaced numbers in sequences.
plt.plot(num_seq, sigmoid(num_seq),'r') # the 'r'-parameter for 'red'.
plt.xlabel('x')
plt.ylabel('y')
plt.title('sigmoid function')
plt.grid()
plt.show() 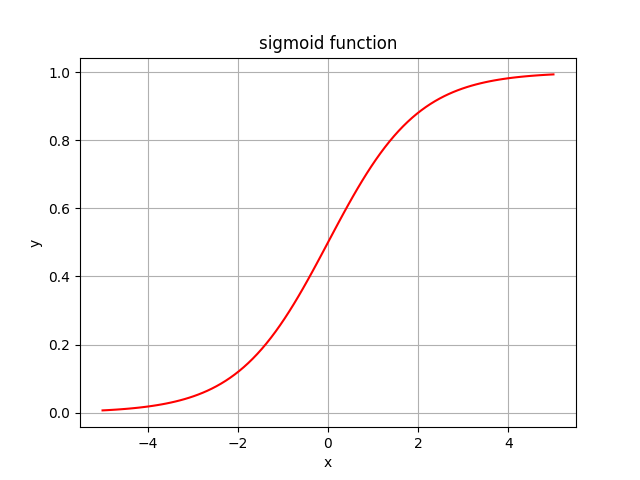
What are the drawbacks of the sigmoid function?
If you look at the picture of the sigmoid curve above, you'll notice that there are regions on the graph where the function doesn't change much. That means that the gradient at that region is going to be very small. The problem of "vanishing gradient" rises: when gradients become very small, the weight update stays the same or changes extremely slowly. When the update of weights stops, the learning stops.
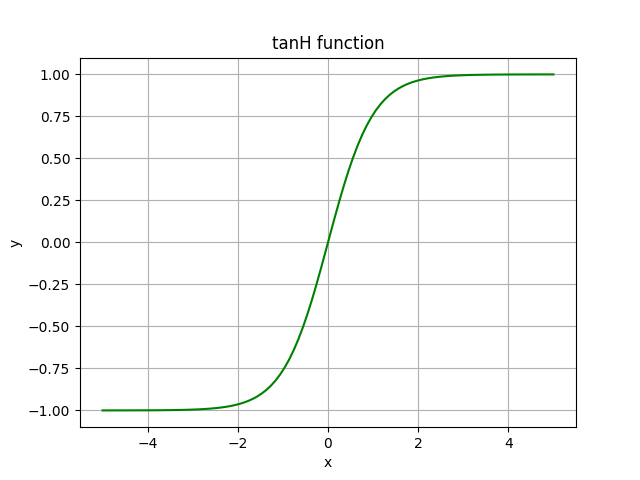
TanH Function (Hyperbolic Tangent)
TanH looks similar to sigmoid. In fact, it is the scaled version of the sigmoid function. The range of the tanH function is [-1;1].

In comparison to sigmoid, tanH has stronger gradients (derivatives are steeper): if the data is centered around 0, the derivatives are higher. Dependent on the gradient strength you need, you choose between the both. But similar to sigmoid, tanH is susceptible to the same vanishing gradient problem.
Implementation of the TanH Function
import numpy as np
import matplotlib.pyplot as plt
def tanH(num):
return (2 / (1 + np.exp(-2*num))) - 1
num_seq = np.linspace(-5, 5, 100)
plt.plot(num_seq, tanH(num_seq),'g')
plt.xlabel('x')
plt.ylabel('y')
plt.title('tanH function')
plt.grid()
plt.show()
Rectified Linear Unit (ReLu)

ReLu function gives the input as the output if the input is positive and 0 if the input is negative.
It is widely used in hidden layers.
If you look at the graph above, you may think that this function is linear. But it is not! In fact, all combinations of ReLu are non-linear.
ReLu is computationally light, because it outputs max(input, 0), so it doesn't have massive calculations and easy to implement mathematically.
If we have a neural network, where for 60% of the network ReLu outputs 0 (zero for negative values). That means less neurons fire (get activated), so we have a sparse activation, which means the network gets lighter.
Implementation of the ReLu Function
import numpy as np
import matplotlib.pyplot as plt
def relu(num):
return np.maximum(num, 0)
num_seq = np.linspace(-5, 5, 100)
plt.plot(num_seq, relu(num_seq),'b')
plt.xlabel('x')
plt.ylabel('y')
plt.title('relu function')
plt.grid()
plt.show()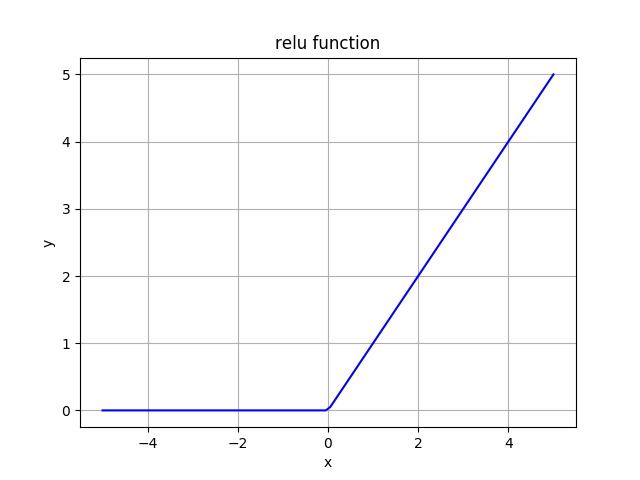
What are potential problems with ReLu?
The range of ReLu is [0, inf), which means that the function can explode the activation because there is no boundary.
If you look at the ReLu graph above, you will notice that horizontal line (for negative x or x=0) where the ReLu output is 0, which indicates that the gradient goes towards 0. That denotes, the gradient in this span becomes 0 and the weights won't be tweaked during descent. If the weights update stops (or becomes significantly slow), the learning stops. If the gradient is 0, that means, nothing changes. The neurons which are in such state stop reacting to changes in the error. This is what we know as Dying ReLu Problem. This problem causes a part of the neurons "die" as they won't respond. This makes neural network passive and even static.
There is an approach to the dying ReLu problem, the so called "Leaky ReLu". This Leaky ReLu allows a some "leakage" for an input variable less than 0. In other words, we take the horizontal line and convert it into a non-horizontal element by inclining it. The key idea is: allow gradients equal 0.

Softmax
Softmax is often used in multiclass classification tasks. The output of the softmax is big if the input (also called logit or score) is big. If the input is small, the output will also be small.

Softmax is widely used in the output layer. It is suitable for classification or linear regression type of tasks.
Softmax takes in a vector with logits (scores) and outputs a vector with probabilities which sum up to 1. The output represents a probability distribution (or categorical distribution) of possible outcomes. The most important task for softmax is: it turns numbers into probabilities which is great for probability analysis.
We called the input values for softmax logits several times. Logits are numerical values which are the output of the last hidden layer. So logits are scores from the last layer before activation (e.g. softmax) comes in.
If you look at the formula, you'll see that it sums over all samples in input. That means: a considerable drawback of softmax is that it takes linear time to accomplish a task O(n).
import numpy as np
import matplotlib.pyplot as plt
def softmax(num):
return np.exp(num) / np.sum(np.exp(num), axis=0)
# Axes are needed for multi-dimensional arrays.
# A 2-dimensional array, for example, has two axes (x,y): the first one (y) is vertical and goes downwards across the rows (axis 0).
# The second one is horizontal and goes across columns (axis 1).
num_seq = np.linspace(-5, 5, 100)
plt.plot(num_seq, softmax(num_seq),'m')
plt.xlabel('x')
plt.ylabel('y')
plt.title('softmax function')
plt.grid()
plt.show()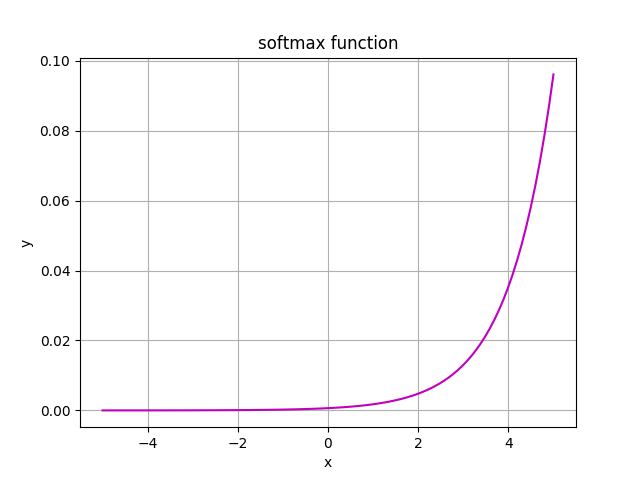
Which activation function should I chose?
Can I just always use ReLu or Sigmoid or tanH? Well, it depends on the task you have. Generally speaking, you should choose the kind of an activation function which approximates the function faster and leads to faster training. You can even customize your own activation function and use it! As a rule of thumb: for the start take ReLu and test it. As a rule, ReLu works fine as a general approximator.
Further recommended readings:
Activation Functions Implementation on Github
Check out the article on Backpropagation ...
... or on Recurrent Neural Networks (RNNs) as well
😄

