Introduction to Statistics
Measures of Variability (Spread, Dispersion)
The second group we use in descriptive statistics to describe data is the measures of variability. Sometimes also called measures of spread or just dispersion. As the name reveals, here our goal is to describe the variability within the data or the extend of stretching or squeezing in the data. In other words, when we use measures of variability, we want to know how spread out the data is.

the distribution number 1 has the lowest variability
Range
The range is one of the measures of variability that is intuitively easy to understand. It's the difference between the smallest and the largest term in the data set.

Interquartile Range (IQR)
First of all, what is a quartile? In simple words, a quartile is a representation of the data split. Quartile comes from "quarter", so a quartile divides data (namely, distribution) into four equal parts.
- The Q1 (the lower quartile) denotes the first quartile and is essentially the middle number between the median of the data and the smallest number in the data.
- The Q2 (50 % of the rest values lie below and the other 50 % above) is the second quartile and is in fact the median of the data set.
- The Q3 (the upper quartile) is the third quartile and is the number in the middle between the highest value of the data and the median.
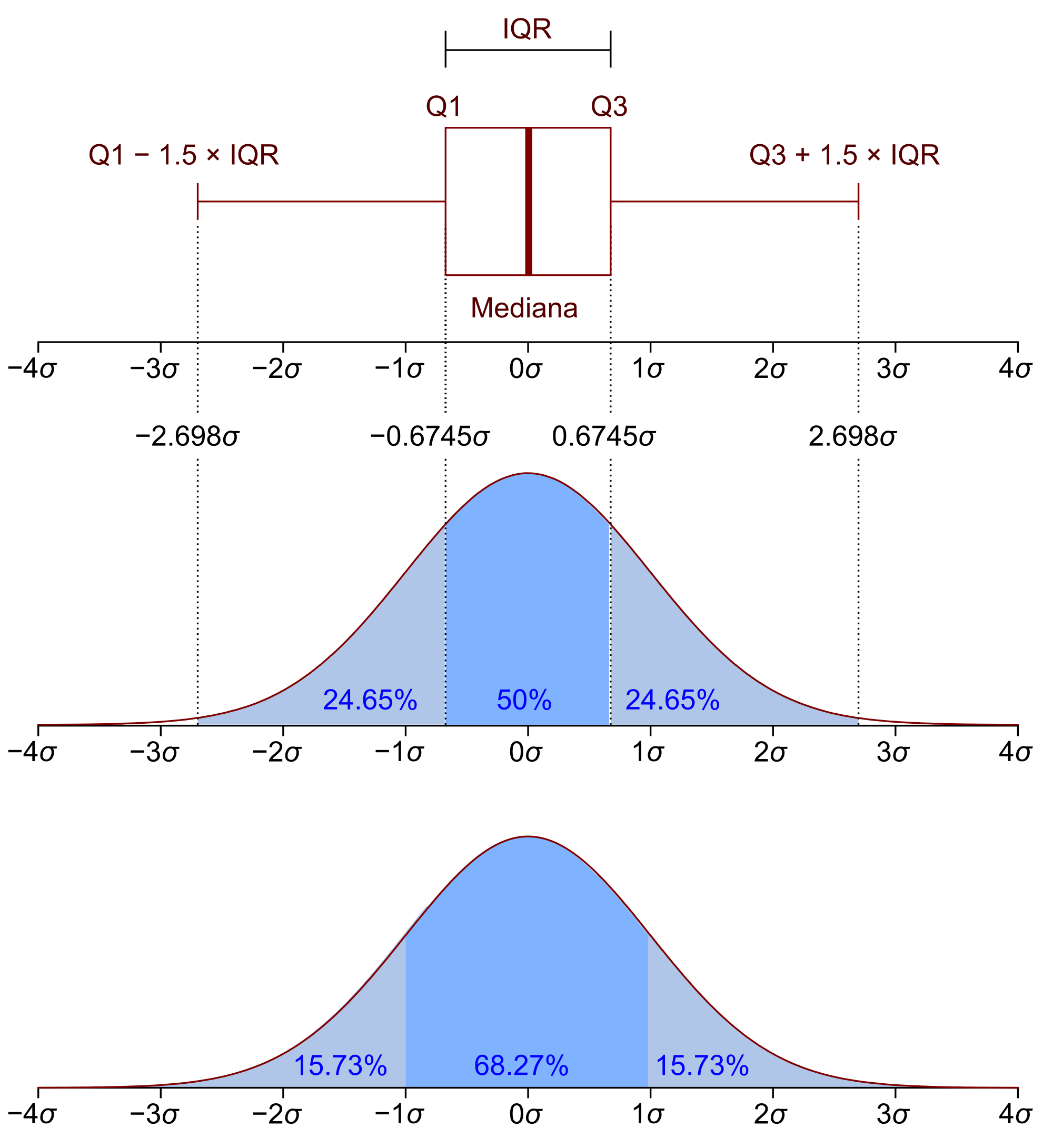
Source wiki
The IQR measure shows how widespread the interval is, in which the middle 50 % of all the values lie.
A general procedure to find IQR would be:
- sort the data
- find the median in the whole data
- find the difference between the middle of the first half and the middle of the second half. In other words, find the difference between the medians from the first and the second parts respectively.
Let's look at an example:
Out data set can look like this:

Step 1: Sort the data set:

Step 2: Determine the median of the data:

Step 3: Find the difference between the middle of the second part and the middle of the first part

Pay attention:
Quartile is often confused with quantile ... They are similar but not the same. Look at the short note below to see the difference:
Note about quartile vs. quantile :
Quantile (from "quantity") is a point at which a distribution is divided into equal parts. Strictly speaking the median is a quantile because it (the median) divides the complete data set into two equal groups: the first one is lower than the median (the first 50%) and the second one is above the median (the second 50%).
Quartile is one type of quantile. Quartile divide the data set (the distribution) into four equally sized parts. So, for example, one quartile is equal to 0.25 quantile.
Standard Deviation (SD)
The standard deviation (SD) describes how data is spread out going from the mean. SD measures dispersion (variance) of a data set.
If the data points are closer to the mean, then we observe low SD :

If the data points have a wide spread, then we observe high SD :

The formula for the SD is:
Variance
if we look at the definition from Wikipedia, we read:
"it measures how far a set of (random) numbers are spread out from their average value", Wikipedia (Variance)
And what's the difference from the standard deviation? Well, basically there is no big mathematical differences between the standard deviation and the variance. So, in our statistical analysis we can sometimes interchange both. We use the variance to calculate the data spread. The variance give us a measure of how far the values are distributed from each other starting from the mean but we can also use the SD for this task.
We can present the variance as the square root of the Standard Deviation:

Variance, SD and interquartile range are all used to measure statistical dispersion. Both variance and SD are applied to measure the spread around a data set and both of them tell us the spread of a data set around the mean.
Distributions
We will cover the topic of probability in the Part II more in detail. But for now, a probability distribution summarizes all outcomes of an experiment.
Normal Distribution
The normal distribution is often called Gaussian or Laplace-Gauss Distribution. It is a continuous probability distribution.
Continuous values are for example person's age, weight, height, stock prices, etc...

Look closely at the normal distribution graph above. Did you notice that the distribution's "tails" never touch the x-axis? This we call horizontal asymptote. Asymptote is some hypothetical line which touches the curve at some point in infinity. Which basically means, the curve approaches the line but never actually reaches and touches it.
The curve can only approximate the x-axis but never reach it because we cannot realistically be 100% sure about any result. If we measure the area under the curve at some "tail-point", we see that it is very small but still existent. In other words the area under the curve depicts the probability of getting a particular value.
As we mentioned above the measures of central tendency are all equal with the normal distribution. They are all equal because most of the data is placed around the center and the total area under the curve is equal to 1 which respects the probability measure.

Data Dispersion
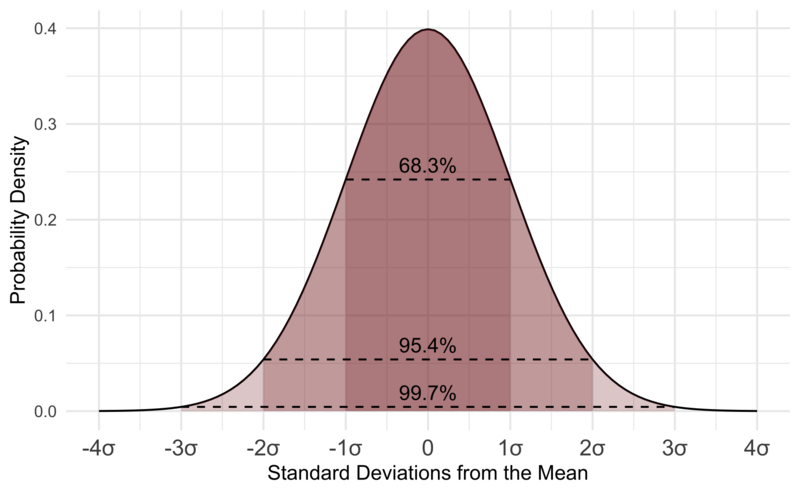
Source wikiwand
Inspect the image above. We can see that approx. the 68-69 % of the whole data set is within the first standard deviation and approx. 95 % in the second. And if we look at all three standard deviations, we cover almost 100 % of the whole data set.
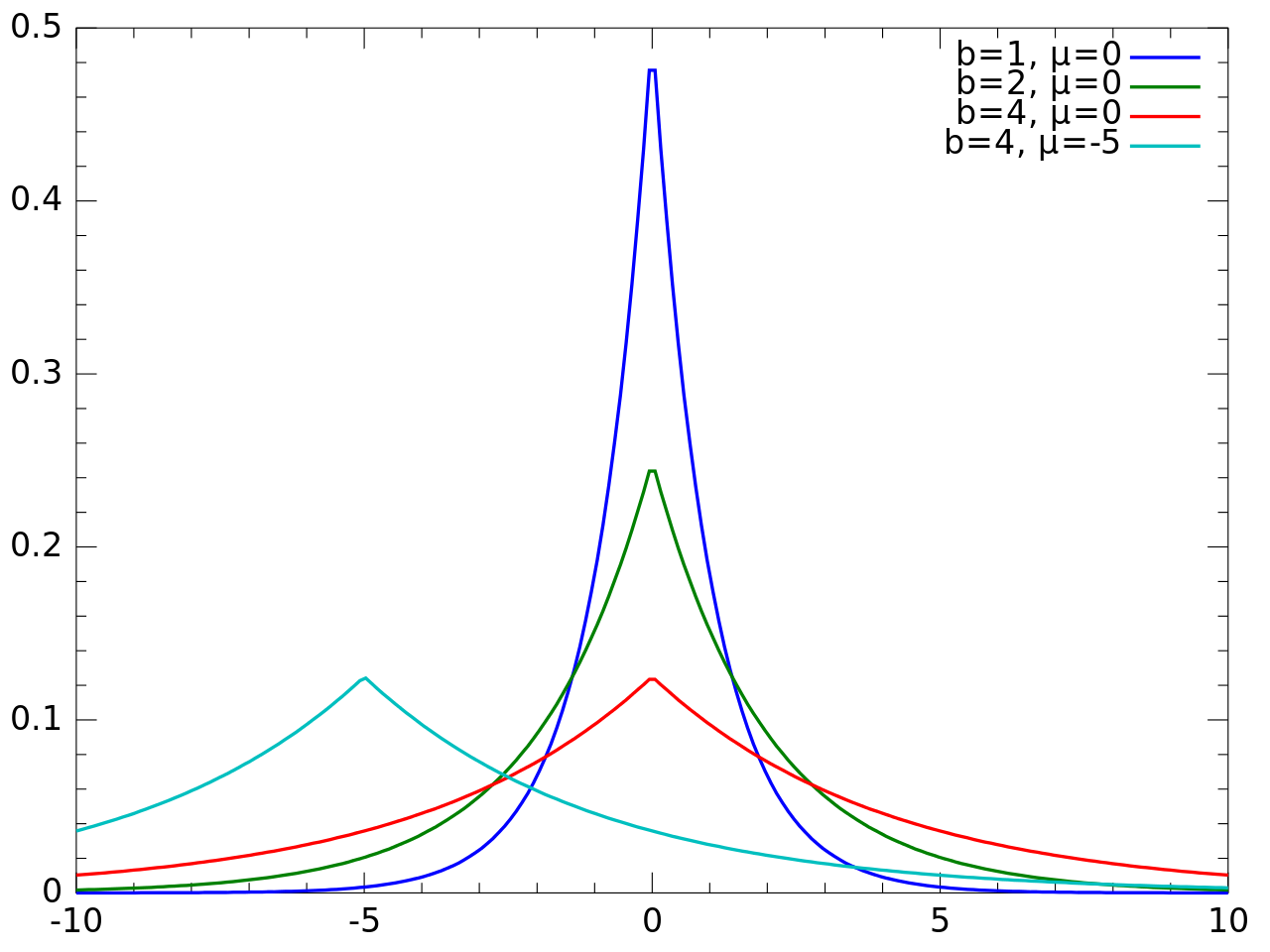
Laplace Distribution
Another continuous probability distribution is the Laplace distribution. This kind of distribution is frequently associated with the exponential distribution because we can view the Laplace distribution as if it would combine two exponential distributions.
Binomial Distribution
The binomial distribution is a discrete probability distribution. Discrete values are always certain and can be placed in certain categories, for example the gender of a person, income (low, medium, high), grades (bad, satisfactory, good, excellent), civil status (single, married, divorced), etc ...

In contrast to the normal distribution, the binomial distribution takes only a limited number of values hence, it is discrete.

Binomial Distribution: discrete probability distribution

Normal Distribution: continuous probability distribution
Uniform Distribution

The uniform distribution (also rectangular distribution) is a kind of a distribution that has a constant probability. The uniform distribution is symmetric in its nature and has all its intervals of the same length.
Conclusion for Part I and Part II
In these two parts we learned about two major branches in statistics: descriptive and inferential. We've seen what are the measures of central tendency and the measures of variability and got to know some types of probability distributions.
In the third part of this article, we're going to learn more about the three axioms of the probability theory and different probability types.
Read The Part III next :)
Further recommended readings:
Introduction to Statistics Part I


