Neural Networks
To start with, Neural Networks provide us a possibility to do machine learning (ML). Neural Network is a program which performs a task by analyzing training data. There are many types and kinds of machine learning models and algorithms, like e.g. Linear or Logistic Regression, Perceptron, Feed Forward, LSTM, Convolutional Neural Network (CNN), Recurrent Neural Network (RNN), Support Vector Machines (SVM), and many more ...
Neural Networks are often called universal function approximators. That means, using NNs we could possibly solve any set of problems. That is, if we can reduce a problem (task) to some function, we can approximate it with the help of Neural Networks.
Typical tasks for NNs include: forecasting, recommendation systems, risk management, anomaly detection, time series predictions and natural language understanding.
Machine Learning same as Neural Networks?
Machine Learning (ML) is a broader term as Neural Networks. A neural network (sometimes also "artificial neural network") is a type of machine learning.
Generally speaking, a machine learning algorithm consists of the following stages:
- explore and clean data
- preprocess data (e.g. make it numerical)
- define the model (=algorithm) architecture (set up the layers)
- compile the model (set up the optimizer, the loss function and metrics)
- training the model (also "fitting the model" or "estimating parameters")
- test the model (also "evaluating")
Machine Learning Lingo:
You should get used to the fact that one term in ML might have maybe five different names. That is why, here some frequent terms used in ML:
- label - the desired outcome we want to predict. In simple linear regression it corresponds to the y-variable.
- feature (also "attribute" or "dimension") - the input data, corresponds to the x-variable. Examples of features for spam classification: words in an e-mail, number of exclamation marks, sender's address, etc...
- model (algorithm) - defines the relationship between features and labels.
- weights - a feature coefficient. The main idea of training a model is to find the ideal weight for every feature. Weights connect each neuron in one layer to every neuron in the next layer.
- layer - a structure that receives weighted input, transforms it with a non-linear function and then passes these values as output to the next layer. There are an input layer, a hidden layer and an output layer.
Supervised vs. Unsupervised Learning
In supervised learning the data we give ("feed into") the neural network has been already labeled. That is, the model learns on data with an label, which is the right "answer" we want to predict in the end. So, the model learns from labeled examples.
In contrast, in unsupervised learning unlabeled data is used. The model tries to make sense of this data by extracting patterns unattended. So we don't need e.g. a human annotator for this type of machine learning.
There are Discrete/Continuous Supervised Learning and Discrete/Continuous Unsupervised Learning. Discrete means the variable is of either concrete category: yes or no, cat or dog, red or green or blue. Whereas, continuous means ongoing change in variables like age, height, stock price, price of a house. Those values are constantly changing.
Examples of: discrete supervised learning would be classification or categorization problems. Continuous supervised learning: regression problems like Linear Regression.
Examples of: discrete unsupervised learning would be clustering, where we have particular groups or "clusters". Continuous unsupervised learning would be Dimensionality Reduction.
Data Splitting
When building a machine learning model, we usually split our data into two kinds of sets:
- Training set
- Test set
A training set contains a "right" output (label). The model learns on this data to be able to generalize on unseen data.
A test set is used to give us an accuracy estimation expected on new, previously unseen data. The test set measures how good or bad the model is on new unseen data, so we can measure how good the model generalizes because of this unbiased result.
It is advisable to even split data in three sets:
- Training set
- Development set (sometimes also "validation set")
- Test set
A development set is used to evaluate the model with different hyperparameters. We can improve our model's performance by tweaking its hyperparameters (learning rate, number of iterations, batch size, loss function, etc...).
We normally have to specify model's hyperparameters manually. Model's parameters are often not set manually but are determined automatically by the model.
In an ideal situation we would develop a model using a training set. Then we tweak model's hyperparameters in a way, that it performs good on a development set. In the end, we would finally check the model's performance on a test set, which is brand new and was never seen before by our model, so we can get the best unbiased judgment.
Overfitting vs. Underfitting
Overfitting happens when our trained model cannot generalize well on previously unseen data. An "overfitted" model will be extremely precise on the training data but will show a very poor accuracy on new data. With overfitting we can't generalize the output and can't reason on other data, which is our prior goal. Overfitting often happens in complex models with a lot of features. That also means, the more hidden neurons, the higher the risk of overfitting. In this case, the system didn't learn to generalize data but stores/memorizes the data patterns and any noise contained in them. Overfitting may also occur due to homogeneous data. That means, we should keep data diverse.
On the contrary, underfitting happens when the accuracy on the development set is higher as the accuracy on the train set. If underfitting occurs, the model fails to recognize patterns in data. As well as with overfitting, an underfitted model cannot be generalized to novel data. Underfitting often occurs with very simple models where the model lacks of predictors (also called "independent variables"). Underfitting may happen when, we try fitting (training) a linear model (e.g. linear regression) to data that is not linear. Such model will definitely output faulty predictions.
In general, we can reduce overfitting/underfitting by splitting our data into train/validation/test sets. For overfitting reduction we can add more data to our training set. Regularization techniques as Dropout and L1/L2 Regularization are also a good help in reducing overfitting.
Overfitting Reduction: Regularization
To overcome overfitting we can use regularization techniques:
Dropout
when we use dropout, we randomly delete some number of neurons (also called "activations") during training. Then, during testing, we use all neurons but we also reduce them by a number of missing neurons during training.
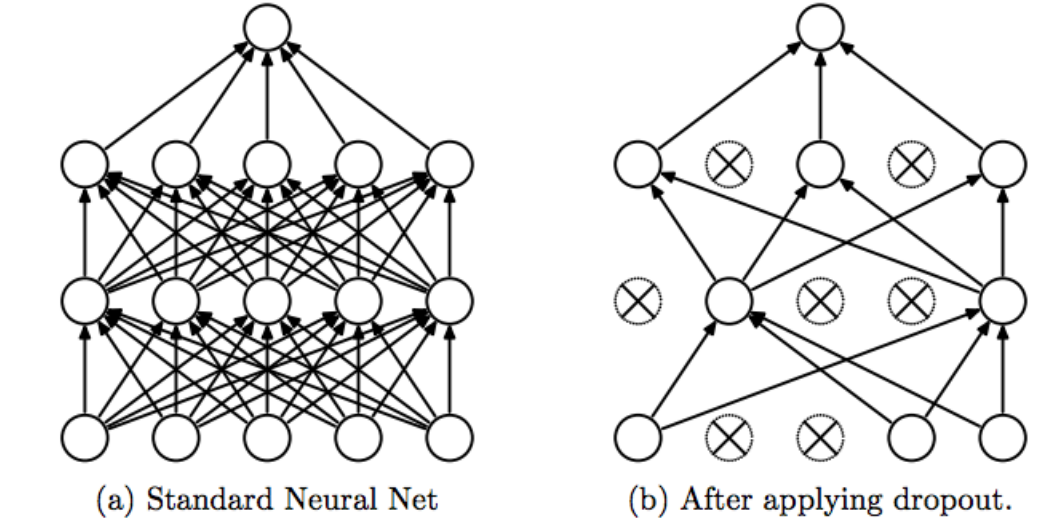
Srivastava, Nitish, et al. "Dropout: a simple way to prevent neural networks from overfitting", JMLR 2014
Feel free to read the original paper.
The problem with dropout is: it causes the information to get lost and may even result in underfitting.
Regularization assumes that smaller weights create a simpler model, helping to prevent overfitting.
L1 Regularization
The L1 regularization penalizes the algorithm for keeping weights that are not zeros. With the L1 regularization we try to zero out not useful weights, so we don't have to deal with unnecessary feature crosses. "Feature crosses" means: when we multiply (or "cross") two or more features, it results in vectors having more and more dimensions. More dimensions in data means more RAM capacity is needed, more computation time is required and model's complexity grows. Zeroing out some features will save RAM and reduce noise in the model. By deactivating non-informative features, we can make our network less complex, which means less overfitting.
The problem with L1: it produces models that are not capable of learning more complex patterns.
L2 Regularization
The L2 regularization makes the weights very small but does not force them to become 0 as in L1, so L2 has no feature selection built in thus L2 cannot find non-informative features.
Feel free to do some exercises here to strengthen your knowledge.
Learning
The actual "learning" happens when the model's parameters are updated. Those parameters can be e.g. weights in NN, support vectors in SVM, coefficients in a Linear / Logistic Regression. The parameters get adjusted in a way that the model's performance can get better. There are many optimization algorithms for ML. One of them is called Gradient Descent. We use Gradient Descent to minimize a function (also cost function or loss function) by moving towards the steepest descent. How we move and in which direction is defined by the negative of the gradient.
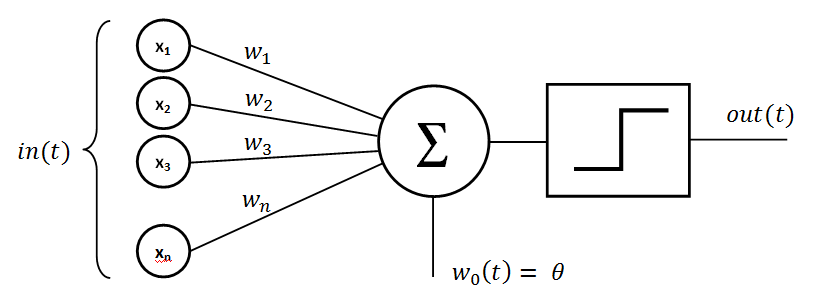
Perceptron
Perceptron is one of the first neural network models. The perceptron algorithm creates "associations" between input stimulations and the necessary response at the output. The perceptron sums up the weighted input values. These values are normally in a form of a vector. Then we "activate" this sum with a function and, in the end, transfer it to the output layer.
Feedforward
Feedforward Neural Networks are in essence multilayer perceptrons. The aim is, the same as said before, to approximate some function.
The model is called "feedforward" because information passes right through: from the input, through the intermediate calculations, and lastly to the output. There are no feedback links in which outputs of the model are fed back into the model again and again. If feedforward neural networks are extended to add feedback connections, they become Recurrent Neural Networks.
Layers: (one layer has one input vector)

where x values are the initial input; w values are the weights; N are the neurons and σ is the sigmoid function. Notice how the output from the first layer (y) becomes input for the second one and so on. At the end of the network we have an s value which is in this case a scalar.
To calculate an output from each layer, we use following formula: activation(input vec * weight vec)
To compute the y-vector we do following:
y1 = sigma(x*w)
y2 = sigma(x*w)
y3 = sigma(x*w)
We can also stack weight vectors w together and make a weight matrix :

Now when we have a weight matrix, we can accomplish our computations much faster.
Conclusion
The initial aim of neural network idea was to solve problems in the similar manner that a human brain would. Nevertheless, NN models were gradually defined to perform certain tasks, leading to deviations from biology.
Further recommended readings:

