Recurrent Neural Networks
RNN vs. Feed Forward
Feed Forward networks originate from the mid. 50s. The network is fully connected and each hidden layer has its own set of weights and biases. The main restriction here is that the set of weights and biases is not shared across all the layers. In a RNN model independent activations are converted into dependent ones, which means that the set of weights and biases is provided to all the layers. So, the parameters are shared across all time steps in a RNN model. That means, the gradient depends not only on the current calculations but on the previous calculations as well.
In a RNN each output serves as an input for the next hidden layer.

RNN Model

Feed Forward Model
Normally Feed Forward neural networks are trained with the help of backpropagation.
Recurrent Neural Network
The main task RNNs are used for, is to operate on data sequences like speech, video, stock market prices, etc. The network analyzes one element at a time, while keeping a "memory" of what was earlier in the sequence.
Recurrent means the output at the present (current) time step becomes the input to the next time step. The model considers not just the current input, but also what it remembers about the preceding elements at each time step in the sequence.
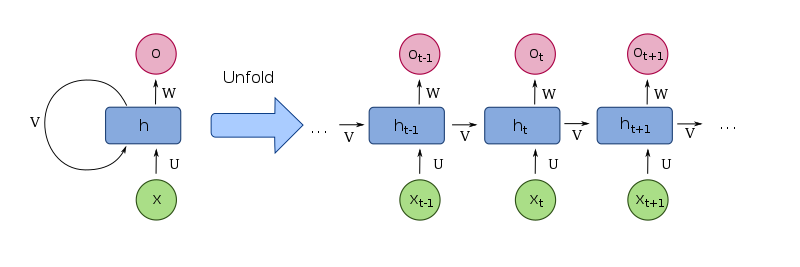
Unfolded Recurrent Neural Network
Such memory structure enables the network model to learn long-term dependencies in a sequence. That means, the model considers the whole context while making a prediction for the next element in a sequence. RNNs were developed to imitate the way how humans analyze sequences: we don't analyze words separately from their context but take into account the entire sentence's context to make an adequate response.

Backpropagation and the Chain Rule
We always want the network to assign a greater "confidence" to a desired target. In supervised machine learning we have labels on our data. What we want as a result is: the output label must be the same as the desired "gold" label.
The structure of an RNN consists entirely of differentiable operations we can run backpropagation on. Backpropagation is a recursive application of the chain rule from calculus. We apply this to figure out, in which direction we should adjust every one of the cell's weights to increase the scores of the desired label. We also perform a parameter update at each iteration, that means, we nudge every weight some amount in a calculated gradient direction. We want a higher score for the correct label at the end. As said before, an RNN is more sophisticated as a standard neural network because an RNN shares its parameters internally. A normal RNN has one weight matrix, which also makes the architecture faster than the one of a standard neural network.
Note:
By performing the feed forward pass we compute the loss of the model.
By performing the backward pass we compute the gradient and try to minimize the loss.
Chain Rule
The chain rule is used in Recurrent Neural Networks for backpropagation. The chain rule enables us to find a derivative, when we have a complicated equation, like e.g. a function inside of a larger function, which is inside of a larger function, etc ...
We normally apply the chain rule, when we have to deal with composite functions or also called nested functions.

Summing up: the chain rule is:
- take the derivative of the outside function and leave the inside part as it is.
- multiply it by ...
- ... the derivative of the inside function
If we want a derivative with respect to x , we have to keep taking the derivative of a function, until we have the final derivative with respect to that x .
That means, we can have many functions being nested inside each other. We can have e.g. a function g inside of a function f : y = f(g(x)) . The number of such "foldings" is unlimited because we can also get something like: y = n(k(q(f(g(x))))) . In such example our derivative will be a chain of smaller derivatives multiplied together to get the right value for the overall derivative.
Vanishing Gradient Problem
RNNs are normally trained with the help of backpropagation (e.g. backpropagation through time or BPTT), where the recursive application of the chain rule is used. Unfortunately, vanilla RNNs, that have no complex recurrent cells, suffer from the so called vanishing gradient problem.
The main problem lies in a fact that the error derivatives cannot be backpropagated through the network at each time step without vanishing to zero or sometimes exploding to infinity. That means, the "vanilla" RNN stops learning as the weight update stops and the calculations from the earlier steps become insignificant for the update/learning. If the gradient becomes small once, it drags the whole computation to the small values which become even smaller after more iterations.
Generally speaking, vanishing gradient is not intrinsically a problem of neural networks by themselves but rather an issue of gradient based methods of computations used in neural networks.
Vanishing gradient happens due to use of some activation functions like the sigmoid type (logistic or tanh). Functions like the logistic one (sigmoid) maps the values between 0 and 1 which are small values that are returned and used in the further computation.
That is why, other types of recurrent cells are often utilized in RNN architectures to lessen the effect of vanishing or exploding gradients. Gradient vanishing/exploding problem can be overcome by Long-Short Term Memory or LSTM for short, which learns long-term dependencies.
Long Short Term Memory or LSTM
LSTM is a type of the Recurrent Neural Network, which utilizes a memory cell. The concept of a usual RNN is that it can process sequential information by remembering let's say 10 previous elements of the sequence. It is fine, when we don't need a bigger gap between the relevant information in the context and the current state. But what if we need much more context? If the gap between the current state we want to predict and some sequence place in the context gets bigger, the RNN won't be able to learn how to connect the information from far away in the context to the current state. Fortunately, there is LSTM. LSTM cells allow remembering many more sequences from the past.
An LSTM network consists of a chain of LSTM-units. Each LSTM unit consists of a cell and it consists of an input/output gate and a forget gate. All those components together are also called a memory cell.
The memory cell is an essential part of the LSTM network. Such a memory cell is composed of gates. Those gates are in control of how information is being processed: added or removed. Gates monitor the information flow in a unit. Gates also implement a sigmoid layer. The sigmoid layer outputs the number spam between 1 and 0, where 0 means "0% of the information is coming through" and 1 means "100% of information is coming through".

The ct is the memory cell of the LSTM neuron. The it , ot , ft in the picture are the input, output and forget gates, they control the state of ct . Gates have their own weights and activation functions.
An LSTM cell allows past information to be used at a later time. LSTMs are clearly constructed to avoid the problem of long-term dependencies, like not being able to go even further in the context from the current state we want to predict the output for. LSTMs remember information from long past periods of time by default. They don't learn it in the first palace, they are already programmed to do so.
Conclusion
Dependent on the task, we use RNN or a more powerful type of RNN - LSTM. LSTM includes a "memory cell " that is able to hold information for a long time with the help of its "gates ". LSTM is suitable, when we need to preserve a wide range of long-term dependencies in a sequence and RNNs are good, when we don't need information from long time ago, so the range of "past dependencies" is relatively small.
A recurrent neural network is a very advanced pattern recognition system. RNNs make their predictions based on the elements ordering in a sequence.
Further recommended readings:
Visualizing memorization in RNNs
To learn more about derivatives, check out this article on Gradient Descent and this video on Derivative formulas through geometry

