Partial Derivatives and the Jacobian Matrix
In the beginning was ... the partial derivative
In order to understand the Jacobian and the Hessian matrices, we need, first of all, to grasp the crucial idea of partial derivatives and the so called second partial derivatives.
Partial Derivatives
First of all, let's focus on the question: what is a "normal" derivative? in the first place. Well, the ordinary derivative (d) demonstrates the instantaneous rate of change or in other words the derivative is a tool used to see the whole amount, by which some function is constantly changing through time. We can think of the derivative as of a tangent line's slope at some point on a graph.

To Find The Derivative:
A "standard" derivative is calculated using the power rule. It is a quick method to figure out the derivative of a function. The power rule works always when we can write the equation in a way that each element of the equation is a variable raised to some power. The power rule is applicable even if the exponent is a fraction or negative.

An "ordinary" derivative has the form of: df / dx. The dx part means: a small change in the variable x. And the df part means: the small change in the output of the function f. All together it answers the question: what is the function's change (output) if some change in x (input) has occurred?
All right, and what about partial derivatives ?
A partial derivative is a derivative, in which we focus on change in only one chosen variable (in one part), ignoring all the other variables or namely, keeping them constant.

or a slightly another example:

The Need for Partial Derivatives?
What if the function's input consists of many variables? We use partial derivatives to observe changes in the function. With them we change one of those variables while keeping all the other variables constant.
To demonstrate a more practical example, we need partial derivatives to solve problems in, for example, engineering, where natural physical processes depend on multiple (multivariable) factors, so we use partial differentiation to observe how some quantity changes when one of the factors changes. Partial differentiation allows us to find the relationship between one main factor and each of other two, three, four, etc... variables and how those multiple factors affect the system in respect to the main factor.
But it's still not all 😈 . There are also the so called second partial derivatives
Consider the last example of partial derivatives. There we again see our function with a two-variable input (two-dimensional) x and y: f(x,y) = x3 y . The partial derivatives of this function take a two-variable input as well. This denotes, that we might take the partial derivatives of the partial derivatives. That process is called second partial derivatives.
Read more about Second-Order Partial Derivatives.
The Gradient
The last concept in this article we cover in order to fully understand the idea of the Jacobian and Hessian matrices. I promise, this is the last one 😁 .
The gradient holds all the partial derivatives of a multivariable function. Just for a recap: a multivariable function is a function with multiple inputs, like in f(x,y) we observe x and y (on total two) multiple inputs. There maybe also more than two, three, etc ... Now back to the gradient: the gradient has often a form of a vector which stores partial derivatives of some multivariable function. The main job of the gradient is that it points in the direction of the steepest ascent on some n-dimenional graph.
You might wonder: what is the difference between a gradient and a derivative? Both represent some change in a function ... Well, the differences are:
- The derivative is a number, which shows the rate of change when some point in our function moves in a particular direction. We can visualize the derivative as a slope of a function which goes along some direction on a graph. We use the letter d to denote the derivative.
- The gradient is, on the other hand, a vector which points in the direction of the steepest ascent. We use the symbol ∇ nabla to denote the gradient.
A Recap Note - Important Symbols: use d for the derivative; ∂ for the partial derivative and ∇ for the gradient.
What is a matrix?
Quote: "The Matrix is everywhere. It is all around us..." Morpheus, The Matrix
In simple terms, it is a number-array arranged in columns and rows. We need matrices in various mathematical fields of study, e.g. for a statistical use to demonstrate and organize data. A single row matrix is also called a row vector and a single column matrix, a column vector.
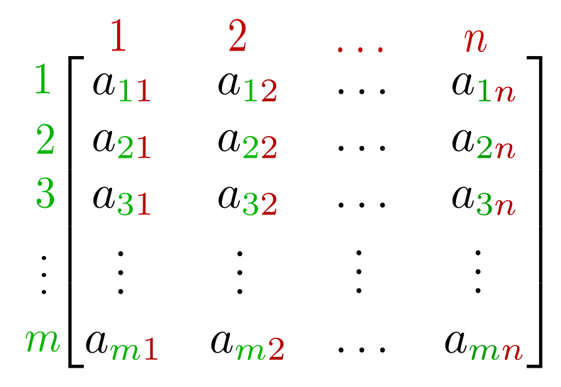
With matrices we are able to organize information in a very compact manner. Matrices can describe linear transformations for us in a precise way. Linear transformations is a crucial concept in mathematics. They are mappings from one function to the other one.
Matrices are widely applied in our daily life. We experience them at work, at university, at home ...😎 . If you happen to use a photoshop software, it will most likely implement matrices to calculate linear transformations for rendering images. With a square matrix we can represent a movement of a geometrical object. In video games, a reflection of an object is possible because of matrices, and so on.
... and the Jacobian Matrix?
Finally, we got here 🤯 . The Jacobian Matrix was introduced by a German-Jewish mathematician Carl Gustav Jacob Jacobi (1804–1851). It is widely applied in vector calculus, where vectors' integration and differentiation play a major role. For example, instead of differentiating/integrating functions which have only one variable, this field of mathematics does the differentiation/integration part with multiple variable instead of only one.
What happens behind the Jacobian matrix transformations is the following: all changes of each vector-component are summed up along each coordinate axis. If we take a function with scalars as its values which are in multiple variables, we can also notice that, the Jacobian matrix of this function is the function's gradient. This very gradient is the derivative of a function with scalar values.
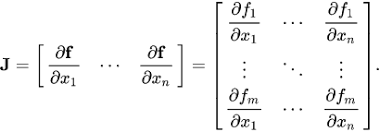
The Jacobian Matrix: source .
The entry for this matrix is usually some variable like for example x. This information denotes that the function is differentiable at this entry x. This crucial feature that we can differentiate this function at some particular entry means, that we can map the whole matrix, visualizing the calculations.
If we know that we can differentiate a function at each entry (a point in a Cartesian plane), then we also know that the Jacobian matrix of this function, we can differentiate, can be seen as a presentation of stretching or rotation (some movement) which our function performs in a locally linear transformation (near that point). The Jacobian matrix basically represents what some transformation looks like at a specific point in some coordinate system.
But what are the differences between Jacobian and the gradient? The gradient, as we said before, is a vector which consists of the partial derivatives of a function. The Jacobian matrix is the matrix which consists of the partial derivatives of a vector function and the vectors in the Jacobian matrix are the gradients of the corresponding elements of the function.
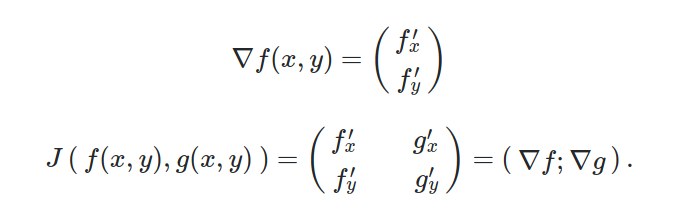
What if we want to transfer vectors from one coordinate system (the Cartesian one) to another coordinate system? We can again apply Jacobian matrices to accomplish this task. We can also summarize and say that the Jacobian matrix is a kind of the gradient generalization in respect to some vector function.
Watch this video for an example of calculating the Jacobian: Find the Jacobian of the Transformation .
The Hessian Matrix
The Hessian matrix or also just Hessian is a square matrix of second order partial derivatives. The Hessian matrix is used to examine the local curvature of a multivariable function. The Hessian matrix was introduced by the German mathematician Ludwig Otto Hesse in the 19th century.
The Hessian (as well as the Jacobian) is also applied to optimize a function (an algorithm, a model). With the help of such matrix we can use iteration to derive optimal coefficients of a function.
Now you may ask yourself: isn't it enough to use only the Jacobian or the Hessian matrix? Aren't they the same? Well, nope. The Jacobian matrix is a square matrix with the first order partial derivatives of some function. The Hessian matrix is the square matrix with the second order partial derivatives of some function. The Jacobian matrix is the matrix of gradients of a function with some vector values. The Hessian matrix is basically the Jacobian matrix of gradients.
We can also take the partial derivatives of the partial derivatives, get the second partial derivatives and produce the Hessian matrix.

The Hessian Matrix: source .
Conclusion
The Jacobian matrix contains information about the local behavior of a function. The Jacobian matrix can be seen as a representation of some local factor of change. It consists of first order partial derivatives. If we take the partial derivatives from the first order partial derivatives, we get the second order partial derivatives, which are used in the Hessian matrix. The Hessian matrix is used for the Second Partial Derivative Test with which we can test, whether a point x is a local maximum, minimum or a so called saddle point .
With the Jacobian matrix we can convert from one coordinate system into another.
Further recommended readings:

