Introduction to Reinforcement Learning
In RL our goal is to find the state-action value in an environment, so that the agent follows the most optimal path and collects the maximum reward.
As we already mentioned in Part I and Part II you can read more about model-based and model-free approaches in RL. The problem with those methods is that they work well on discrete state spaces but perform poorly on continuous ones. As we discussed in Part I, a policy π has a table of the form {(s1, a1), ... , (sn,an)}, so if our Markov Decision Process (MDP) becomes too large because we have a continuous space, we encounter the following problems:
- We have too many states and actions to store in memory.
- To learn the value of each state individually would be too slow.
- It is not possible to represent a continuous state space by a value table.
- What about states that we didn't see yet? We have no way to generalize according to those states.
In which scenarios do we have such continuity? For example in some games like Backgammon, Go, the game of Chess or when we steer an RC Helicopter we may potentially have infinitely many moves, so we are in a continuous state space. We need scalable model-free methods to deal with such continuous environments.
With some games we might encounter an almost infinite amount of states, so if we use a table to store an infinite amount of some values, it quickly becomes inefficient.
Generally speaking, in RL we want to be able to cope with non-stationary targets. Those non-stationary targets are functions that change over time. In control methods, for example, which are based on generalized policy iteration, we often want to learn the qπ function while the policy π changes. The target values of training data samples are non-stationary, even if the policy π remains the same. The targets are often non-stationary if they are generated by bootstrapping methods like DP and TD learning.
Approaches which cannot handle non-stationary values are in general less desirable for effective RL.
So if we have a huge value table with all our states and actions (MDP), we can estimate the value function and perform function approximation:
for the state value function:
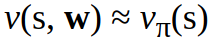
for the state action value function:
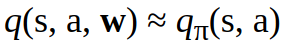
We take an approximate value function which is not a table anymore but a function with a weight vector w. So w in the two equations above w stays for the weight vector. The weight parameter w is updated by applying Monte Carlo (MC) or Temporal Difference (TD) Learning. More on MC and TD methods in Part II.
Value function approximation can be ordered to the model-free control. Model-free control is needed when we want to know how to learn a good policy from experience. With control we can approximate optimal policies.
With value function approximation we can generalize the value estimation. Estimation here means that we don't find the true value but a "close to the true" value, hence we approximate the true value. Intuitively an estimation approach might seem to be inconvenient but it is still computationally faster and generalization works well.

What are typical function approximators?
If we want to approximate some function, we need to choose an approximator. Typical function approximators are e.g. neural networks, Fourier bases, etc...
In this article we will use neural networks as a differentiable function approximator.
Function Approximation with Gradient Descent
One of the most popular neural network optimization techniques is called Gradient Descent. With gradient descent we can find the minimum of a function by iteratively moving in the direction of steepest descent as defined by the negative of the gradient. We normally use the gradient descent optimization algorithm to update the parameters of a machine learning model.
To learn more about Gradient Descent consult the article here.
Let's pick some arbitrary function F(w). This F(w) will be our differentiable function of the parameter w.
Now we define the gradient of the function F(w).

Now in order to find a local minimum of F(w) we have to adjust the weight vector parameter w in the direction of the negative gradient:

Where α is the learning rate.

Some Examples
We have an approximation function v(S, w) which gives some predicted (approximated) value and the true value vπ(S). How does the error that we want to minimize look like? Well, it basically can be represented with the following equation:
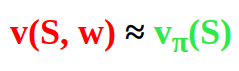
We can try to minimize the Mean Squared Value Error (VE) between the predicted (approximated) value v(S, w) and the true value vπ(S) which builds our objective function.
As a reminder, the formula of MSE is as follows:
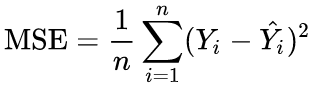
Where Yi is the true value and YÌ‚i is the prediction.
So using our objective function, we get:
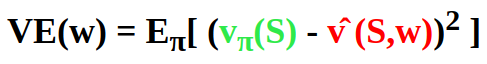
Where vπ(S) is the true value and v(S,w) is the approximation (=prediction).
There are more states than weights. Making one state estimate more accurate means making other state estimates less accurate. That is why we have to decide which states are more important for us. For this we can define the state distribution μ(s) >= 0, Σs μ(s) = 1 . This depicts how much we care about the error in each state s.
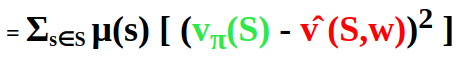
By applying the chain rule, we get the gradient of the objective with respect to its parameter w :
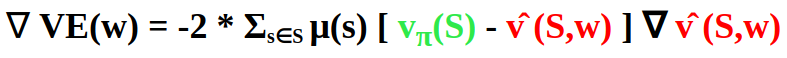
If we use gradient descent, we adjust the parameter w in the direction of the negative gradient by applying the update rule w ← w + Δw where:

The update rule for Stochastic Gradient Descent (SGD) of a single sample S (without a weighting) will look the following way:

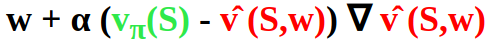
In most cases we do not have the magical true value function vπ(S) ... Nevertheless we have rewards and can use the targets from Monte Carlo or Temporal Difference Learning predictions:
The Monte Carlo target is the return Gt :

So we have:
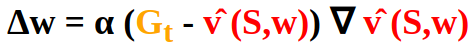
Analogously we have the Temporal Difference Learning target Rt+1 + γ*vÌ‚ (St+1,w):
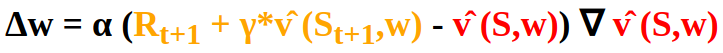
Bootstrapping
What is bootstrapping in the context of RL? Well, bootstrapping methods update estimates of states based on estimates of future states. In other words, such methods update estimates based on other estimates. This concept is called bootstrapping.
With bootstrapping we update targets with their present estimates (like in Dynamic Programming or Temporal Difference Learning) and we do not rely on actual rewards and complete returns (as e.g. in Monte Carlo methods).
With bootstrapping we can achieve faster learning for our model. Faster learning with bootstrapping happens because with bootstrapping the model can learn to recognize a state by repeatedly returning to it. One of possible problems with bootstrapping is that it can make learning less efficient for problems where the state representation is not good enough which results in poor generalization.
The Deadly Triad
There are many possibilities of how our system can output unsatisfying results. Instability of results comes along with the usage of a particular configuration with the three following features:
- Function Approximation
- Bootstrapping
- Off-Policy Training
Such combination within one model is called the deadly triad.
How do we deal with the deadly triad? Well, one possibility would be to find out whether there is one of the three deadly triad components that can be omitted.
What if only two deadly triad elements are present? If there are not all three of them, then instability can be avoided.
Moreover, if all three elements are present, the instability problems appears already with a simple prediction task. So, your RL task or your ML model doesn't have to be complex to suffer from the deadly triad.
Which of the three could be omitted?
It is definitely not advisable to omit function approximation. We still need scalable methods for larger problems with continuous spaces. It could be possible to try Linear Function Approximation instead, but linear function approximation has too many features and parameters, which in turn has its own negative sides.
All right, but what if we replace function approximation with some non-parametric method? Well, the problem here is: the time complexity of non-parametric methods grows with data. Besides non-parametric methods are in general too weak or too expensive.
What about Least Squares Methods? There are some, for example Least Squares Temporal Difference (LSTD). The problem with those methods is that they all have quadratic time complexity and are therefore too computationally expensive for larger problems.
As a result, it's better to keep Function Approximation.
Omitting bootstrapping may be possible. But then we encounter losses in computational efficiency. We will probably try to keep it.
Off-policy learning. Can we do without it good enough? On-policy methods are often suitable as well, so often we can replace an off-policy with an on-policy learning.
As an example, in case of model-free reinforcement learning, we can often apply SARSA (on-policy), rather than Q-learning (off-policy).
Conclusion
Function approximation is a scalable method for applications with continuous state spaces which are much larger than the memory and computational resources we might have.
Further recommended readings:
Part I : Model-Based Reinforcement Learning
Part II : Model-Free Reinforcement Learning
Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto

